一半径R=0.6m的金属圆筒有一圈细窄缝，形状如图所示。圆筒右侧与一个垂直纸面向里的有界匀强磁场相切于P，圆筒接地，圆心O处接正极，正极与圆筒之间的电场类似于正点电荷的电场，正极与圆筒之间电势差U可调。正极附近放有一粒子源（粒子源与正极O间距离忽略不计）能沿纸面向四周释放比荷q/m=1.5×l05C/kg的带正电粒子（粒子的初速度、重力均不计）。带电粒子经电场加速后从缝中射出进入磁场，已知磁场宽度d=0.4m，磁感应强度B=0.25T。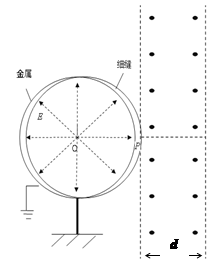
（1）若U=750V，求：①粒子达到细缝处的速度；②若有一粒子在磁场中运动的时间最短，求此粒子飞出磁场时与右边界的夹角大小。
（2）只要电势差U在合适的范围内变化，总有从向沿某一方向射出粒子经过磁场后又回到O处，求电势差U合适的范围。
质量为M="1000" kg的汽车，在半径为R=25m的水平圆形路面转弯，汽车所受的静摩擦力提供转弯时的向心力，静摩擦力的最大值为重力的0.3倍。为避免汽车发生离心运动酿成事故，试求汽车安全行驶的速度范围。(g取10 m/s2 )
如图所示，质量为m的物体沿倾角为α的粗糙斜面下滑了一段距离s，物体与斜面间的动摩擦因数为μ，试求物体所受各力在下滑过程中对物体所做的功及这些力所做的总功.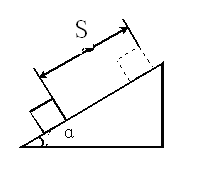
如图所示，轨道ABCD的AB段为一半径R =0.2m的光滑1/4圆形轨道，BC段为高h =5m的竖直轨道，CD段为水平轨道。一质量为0.1kg的小球由A点从静止开始下滑到B点时速度的大小为2m/s，离开B点后做平抛运动（g取10m/s2），求：
（1）、小球离开B点后，在CD轨道上的落地点到C的水平距离。
（2）、小球到达B点时对圆形轨道的压力大小。
（3）、如果在BCD轨道上再放置一个倾角θ＝45°的斜面（如图中虚线所示），那么小球离开B点后能否落到斜面上？如果不能，请说明理由；如果能，请求出它第一次落在斜面上的位置。
一根长为L的轻杆，一端固定一质量为m的小球A，另一端固定在水平转动轴上.现使小球绕杆的另一端的转轴在竖直平面内做圆周运动，如图.试求:
（1）假设小球转至最低点时，小球的速度大小为
，求此时小球对的杆作用力；
（2）假设小球转至最高点时，小球的速度大小为
，此时杆对小球的作用力是支持力还是拉力？此力为多大？
一个小球从倾角为θ的斜面上A点以水平速度v0抛出，不计空气阻力，求：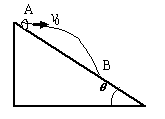
(1) 自抛出至落到斜面需要的时间；
(2) 落到斜面上的B点到抛出点A的距离；