(9分) 用如图所示的装置测量某种矿物质的密度，操作步骤和实验数据如下：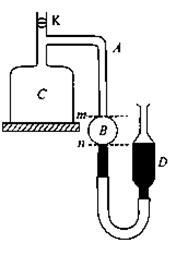
a．打开阀门K，使管A、容器C、容器B和大气相通。上下移动D，使水银面与刻度n对齐；
b．关闭K，向上举D，使水银面达到刻度m处。这时测得B、D两管内水银面高度差h1=19.0cm；
c．打开K，把m=400g的矿物质投入C中，使水银面重新与n对齐，然后关闭K；
d．向上举D，使水银面重新到达刻度m处，这时测得B、D两管内水银面高度差h2=20.6cm。
已知容器C 和管A的总体积为VC=1000cm3，求该矿物质的密度。
弹簧振子以O点为平衡位置，在B、C两点间做简谐运动，在t＝0时刻，振子从O、B间的P点以速度v向B点运动；在t＝0.20 s时，振子速度第一次变为－v；在t＝0.50 s时，振子速度第二次变为－v.
(1)求弹簧振子振动周期T.
(2)若B、C之间的距离为25 cm，求振子在4.00 s内通过的路程．
(3)若B、C之间的距离为25 cm.从平衡位置计时，写出弹簧振子位移表达式，并画出弹簧振子的振动图象．
某发电站的输出功率为104 kW，输出电压为4 kV，通过理想变压器升压后向80 km远处供电．已知输电导线的电阻率为ρ＝2.4×10－8 Ω·m，导线横截面积为1.5×10－4 m2，输电线路损失的功率为输出功率的4%，求：
(1)升压变压器的输出电压；
(2)输电线路上的电压损失．
如图10－1－14所示，匀强磁场的磁感应强度B＝0.5 T，边长为L＝10 cm的正方形线圈abcd共100匝，线圈电阻r＝1 Ω，线圈绕垂直于磁感线的对称轴OO′匀速转动，角速度为ω＝2π rad/s，外电路电阻R＝4 Ω，求：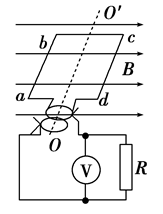
图10－1－14
(1)转动过程中感应电动势的最大值；
(2)由图示位置(线圈平面与磁感线平行)转过60°角时的瞬时感应电动势；
(3)由图示位置转过60°角的过程中产生的平均感应电动势；
(4)交流电压表的示数；
(5)转动一周外力做的功；
(6) 
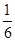周期内通过R的电荷量为多少？
如图9－3－15所示，两根电阻忽略不计的相同金属直角导轨相距为l，它们各有一边在同一水平面内，另一边垂直于水平面，且都是足够长．两金属杆ab、cd与导轨垂直接触形成闭合回路，杆与导轨之间的动摩擦因数均为μ，且最大静摩擦力与滑动摩擦力相等．回路总电阻为R，整个装置处于竖直向上的匀强磁场中．现使杆ab受到F＝5.5＋1.25t(N)的水平外力作用，从水平导轨的最左端由静止开始向右做匀加速直线运动，杆cd也同时从静止开始沿竖直导轨向下运动．已知：l＝2 m，mab＝1 kg，mcd＝0.1 kg，R＝0.4 Ω，μ＝0.5，g取10 m/s2.求：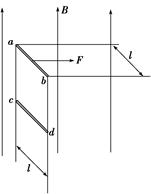
图9－3－15
(1)磁感应强度B的大小；
(2)cd杆下落过程达最大速度时，ab杆的速度大小．
如图9－2－13所示，a、b灯分别标有“36 V 40 W”和“36 V 25 W”，闭合电键，调节R，能使a、b都正常发光．断开电键后重做实验，电键闭合后看到的现象是什么？稳定后哪只灯较亮？再断开电键，又将看到什么现象？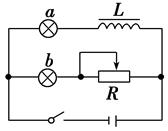 
图9－2－13