如图所示,光滑导轨abc与fed相距l=0.1m,其中ab、fe段是倾角θ=60°的直轨道,bc、ed段是半径r=0.6m的圆弧轨道且与ab、fe相切,轨道末端c、d点切线与一放置在光滑水平地面上、质量M=2kg的木板上表面平滑连接。在abef间有垂直于轨道平面向下、 的匀强磁场,定值电阻R=1Ω。把质量为m=1kg、电阻不计的金属杆从距b、e高h=1m的导轨上静止释放,杆在直轨道上先加速后匀速下滑。如果杆与木板间摩擦因数μ=0.2,取g=10m/s2,求:
的匀强磁场,定值电阻R=1Ω。把质量为m=1kg、电阻不计的金属杆从距b、e高h=1m的导轨上静止释放,杆在直轨道上先加速后匀速下滑。如果杆与木板间摩擦因数μ=0.2,取g=10m/s2,求:

(1)杆运动到cd时对轨道的压力F大小及杆由静止下滑到cd的过程中R上产生的焦耳热Q;
(2)要使杆不从木板上掉下的木板最小长度s。
质量m=2×103kg,汽车以 的速度通过某凸形桥的最高点时,受到桥面的支持力N=1.5×104N,取g=10m/s2,则桥面的半径为多少?当车速
的速度通过某凸形桥的最高点时,受到桥面的支持力N=1.5×104N,取g=10m/s2,则桥面的半径为多少?当车速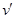 为多大时,车在桥最高点时对桥面的压力恰好为零?
为多大时,车在桥最高点时对桥面的压力恰好为零?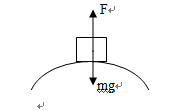
英国某媒体推测:在2020年之前人类有望登上火星,而登上火星的第一人很可能是中国人。假如你有幸成为人类登陆火星的第一人,乘坐我国自行研制的代表世界领先水平的神舟x号宇宙飞船,通过长途旅行终于亲眼目睹了美丽的火星。为了熟悉火星的环境,你乘坐的x号宇宙飞船绕火星做匀速圆周运动,离火星表面高度为H,飞行了n圈,测得所用的时间为t,已知火星半径R,试求火星表面重力加速度g。
如图所示,轨道ABCD的AB段为半径R=0.4m的四分之一粗糙圆弧形轨道,BC段为高h=5 m的竖直轨道,CD段为水平轨道.一个质量m=1.0kg的小球由A点静止沿下滑,达到B点时,以vB=2.0m/s的水平飞出,(不计空气阻力).取g=10m/s2求:
1)小球从A运动到B过程克服摩擦力做多少功?
2)小球离开B点后,在CD轨道上的落地点到C点的水平距离?
3)小球块落地时的速度大小?
汽车发动机的额定功率为60kW,汽车的质量为5t,汽车在水平路面上行驶时,阻力是5´103N,汽车保持额定功率不变从静止启动(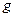 取10m/s2),求:
取10m/s2),求:
1)汽车所能达到的最大速度.
2)当汽车的速度为6m/s时的加速度.
如图所示,α图表示某物体在x轴方向上分速度的v-t图像,b图表示该物体在y轴上分速度图像。求: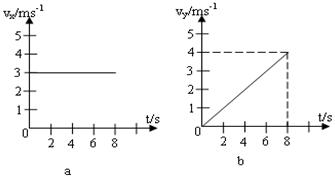
(1)t=8s时物体的速度;
(2)t=4s时物体的位移。