[2014·承德模拟]从装有2个红球和2个白球的口袋内任取2个球,那么互斥但不对立的两个事件是( )
| A.至少有1个白球,都是白球 |
| B.至少有1个白球,至少有1个红球 |
| C.恰有1个白球,恰有2个白球 |
| D.至少有1个白球,都是红球 |
若集合M={y︱x =y,x
=y,x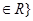 ,集合N={y︱x+y=0,x
,集合N={y︱x+y=0,x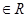 },则M
},则M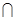 N等于
N等于
A.{y︱y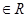 } } |
B.{(-1,1),(0,0)} |
| C.{(0,0)} | D.{x︱x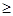 0} 0} |
已知 都是定义在R上的函数,
都是定义在R上的函数, ,且
,且 且
且 ,
, ,对于有穷数列
,对于有穷数列
 ,任取正整数
,任取正整数 ,则前
,则前 项和大于
项和大于 的概率是()
的概率是()
A. |
B. |
C. |
D. |
已知 是公差不为0的等差数列,
是公差不为0的等差数列, 是等比数列,且
是等比数列,且 ,
,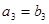 ,
,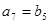 ,
,
那么()
A. |
B.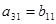 |
C.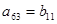 |
D.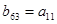 |
从编号为1,2,3,4的四个不同小球中取三个不同的小球放入编号为1,2,3的三个不同盒子,每个盒子放一球,则1号球不放1号盒子且3号球不放3号盒子的放法总数为
| A.10 | B.12 | C.14 | D.16 |
数列 满足
满足 ,若
,若 ,则数列的第2012项为()
,则数列的第2012项为()
A.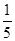 |
B. |
C.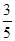 |
D.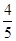 |