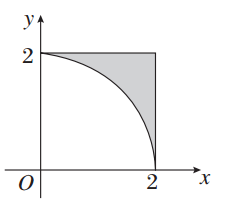
[2012·北京高考]设不等式组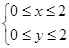
，表示平面区域为D，在区域D内随机取一个点，则此点到坐标原点的距离大于2的概率是( )
A． |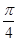
B． |
C． |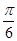
D． |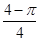
设
，集合
是奇数集，集合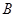
是偶数集。若命题p:
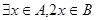，则（）
A． |
B． |
C． |
D． |
在复平面内,复数
对应的点位于（）
| A．第一象限 | B．第二象限 |
| C．第三象限 | D．第四象限 |
已知集合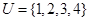
,集合
,
,则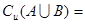
（）
A． |
B． |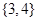
C． |
D． |
设S，T是R的两个非空子集，如果存在一个从S到T的函数y=f（x）满足：（i）T={f（x）|x∈S}；（ii）对任意x1，x2∈S，当x1＜x2时，恒有f（x1）＜f（x2），那么称这两个集合“保序同构”，以下集合对不是“保序同构”的是（）
| A．A=N*，B=N |
| B．A={x|﹣1≤x≤3}，B={x|x=﹣8或0＜x≤10} |
| C．A={x|0＜x＜1}，B=R |
| D．A=Z，B=Q |
满足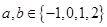
,且关于x的方程
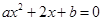有实数解的有序数对
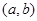的个数为（ ）
| A．14 | B．13 | C．12 | D．10 |