小船从A码头出发,沿垂直于河岸的方向渡河,若河宽为d,渡河速度v船恒定,河水的流速与到河岸的距离成正比,即v水="kx" (x≤d/2,k为常量),要使小船能够到达距A正对岸为s的B码头,则: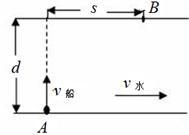
| A.v船应为kd2/4s | B.v船应为kd2/2s |
| C.渡河时间为s/kd | D.渡河时间为2s/kd |
为了研究超重与失重现象,某同学把一体重计放在电梯的地板上,并将一物体放在体重计上随电梯运动并观察体重计示数的变化情况。下表记录了几个特定时刻体重计的示数 (表内时间不表示先后顺序) 若已知t0时刻电梯静止,则:
| 时间 |
t0 |
t1 |
t2 |
t3 |
| 体重计示数(kg) |
45.0 |
50.0 |
40.0 |
45.0 |
A.t1和t2时刻电梯的加速度方向一定相反
B.t1和t2时刻物体的质量并没有发生变化,但所受重力发生了变化
C.t1和t2时刻电梯运动的方向一定相反
D.t3时刻电梯可能向上运动
如图所示,A和B两物块的接触面是水平的,A与B保持相对静止一起沿固定斜面匀速下滑,在下滑过程中B的受力个数为()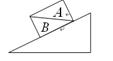
| A.3个 | B.4个 | C.5个 | D.6个 |
一列火车从静止开始做匀加速运动,一人站在第一节车厢前观察:第一节车厢全部通过他需2s,全部车厢通过他需6s,则这列火车的节数为()
| A.3节 | B.5节 | C.7节 | D.9节 |
如图所示,将两个相同的条形磁铁吸在一起,置于水平桌面上,下面说法正确的是()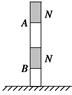
A.B对桌面的压力的大小等于A、B的重力之和
B.B对桌面的压力小于A、B的重力之和
C.A对B的压力的大小等于A的重力
D.A对B的压力大于A的重力
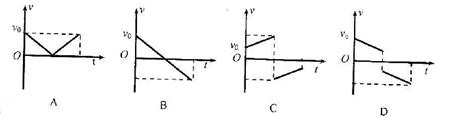
某人将小球以初速度v0竖直向下抛出,经过一段时间小球与地面碰撞,然后向上弹回。以抛出点为原点,竖直向下为正方向,小球与地面碰撞时间极短,碰后立即以原速率弹回,不计空气阻力,则下列图像中能正确描述小球从抛出到弹回的整个过程中速度v随时间t的变化规律的是