如图甲所示为某工厂将生产工件装车的流水线原理示意图。AB段是一光滑曲面，A距离水平段BC的高为H＝1.25m，水平段BC使用水平传送带装置传送工件，已知BC长L＝3m，传送带与工件(可视为质点)间的动摩擦因数为μ＝0.4，皮带轮的半径为R＝0.1m，其上部距车厢底面的高度h＝0.45m。设质量m＝1kg的工件由静止开始从A点下滑，经过B点的拐角处无机械能损失。通过调整皮带轮(不打滑)的转动角速度ω可使工件经C点抛出后落在固定车厢中的不同位置，取g＝10m/s2。
(1)当皮带轮静止时，工件运动到点C时的速度为多大？
(2)皮带轮以ω1＝20rad/s逆时针方向匀速转动，在工件运动到C点的过程中因摩擦而产生的内能为多少？
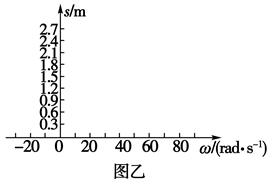
(3)设工件在固定车厢底部的落点到C点的水平距离为s，试在图乙中定量画出s随皮带轮角速度ω变化关系的s－ω图象。(规定皮带轮顺时针方向转动时ω取正值，该问不需要写出计算过程)
如甲图所示，长为4m的水平轨道AB与倾角为37°的足够长斜面BC在B处平滑连接，有一质量为2kg的滑块，从A处由静止开始受水平向右的力F作用，F与位移x的关系按乙图所示规律变化，滑块与AB和BC间的动摩擦因数均为0.5，重力加速度g取l0m/s2。求：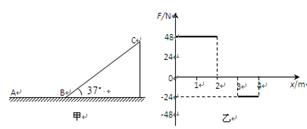
（1）滑块第一次到达B处时的速度大小；
（2）不计滑块在B处的速率变化，滑块到达B点时撤去力F，滑块冲上斜面，则滑块最终静止的位置与B点的距离多大。（sin37°=0.6，cos37°=0.8）
土星上空有许多大小不等的岩石颗粒，其绕土星的运动可视为圆周运动。其中有两个岩石颗粒A和B与土星中心距离分别为rA＝8.0×104 km和r B＝1.2×105 km。忽略所有岩石颗粒间的相互作用。（结果可用根式表示）
（1）求岩石颗粒A和B的线速度之比；（2）求岩石颗粒A和B的周期之比；
一个物体从空中A点做自由落体运动，经过空中B点时速度为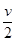
，物体落到地面C点时速度为v。已知B点离地面的高度h=15m，g取10m/s2，求：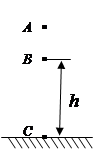
（1）物体落到地面C点时的速度v的大小；
（2）物体在空中运动的时间t；
（3）A点与地面C点的高度H。
如图所示，质量为1kg的物体放在水平地板上，用一原长为8cm的轻质弹簧水平拉该物体，当其刚开始运动时，弹簧的长度为11cm，当弹簧拉着物体匀速前进时，弹簧的长度为10.5cm，已知弹簧的劲度系数k＝200N/m。求：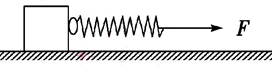
(1)物体所受的最大静摩擦力为多大？
(2)物体与地板间的动摩擦因数是多少？(g均取10m/s2)
一个质点从静止开始做匀加速直线运动。已知它在第4s内的位移是7m。
求：（1）质点运动的加速度；（2）它前进36m所用的时间。