从6名短跑运动员中选出4人参加4×100 m接力赛.试求满足下列条件的参赛方案各有多少种?
(1)甲不能跑第一棒和第四棒;
(2)甲不能跑第一棒,乙不能跑第四棒
已知椭圆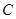 :
: 的离心率为
的离心率为 ,右顶点
,右顶点 是抛物线
是抛物线 的焦点.直线
的焦点.直线 :
: 与椭圆
与椭圆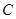 相交于
相交于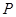 ,
, 两点.
两点.
(Ⅰ)求椭圆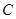 的方程;
的方程;
(Ⅱ)如果 ,点
,点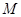 关于直线
关于直线 的对称点
的对称点 在
在 轴上,求
轴上,求 的值.
的值.
如图,在四棱锥P—ABCD中,PA⊥AD,AB∥CD,CD⊥AD,AD =" CD" =" 2AB" = 2,E为PC的中点,DE = EC
(1)求证: 平面
平面
(2)设PA = a,若平面EBD与平面ABCD所成锐二面角的为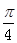 ,求a的值。
,求a的值。
六名学生需依次进行身体体能和外语两个项目的训练及考核。每个项目只有一次补考机会,补考不合格者不能进入下一个项目的训练(即淘汰),若每个学生身体体能考核合格的概率是 ,外语考核合格的概率是
,外语考核合格的概率是 ,假设每一次考试是否合格互不影响.
,假设每一次考试是否合格互不影响.
①求某个学生不被淘汰的概率.
②求6名学生至多有两名被淘汰的概率
③假设某学生不放弃每一次考核的机会,用 表示其参加补考的次数,求随机变量
表示其参加补考的次数,求随机变量 的分布列和数学期望.
的分布列和数学期望.
已知函数 的最大值为2.
的最大值为2.
(1)求函数 在
在 上的单调递减区间;
上的单调递减区间;
(2)△ABC中, ,角A、B、C所对的边分别是a、b、c,且
,角A、B、C所对的边分别是a、b、c,且 ,
,
c=3,求 的值.
的值.
在平面直角坐标系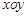 中,圆
中,圆 的参数方程为
的参数方程为 (
( 为参数),直线
为参数),直线 经过点
经过点 ,
,
倾斜角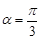 。
。
(1)写出圆的标准方程和直线 的参数方程;
的参数方程;
(2)设 与圆
与圆 相交于
相交于 、
、 两点,求
两点,求 的值
的值