(13分)已知函数 的图象在点
的图象在点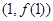 处的切线垂直于
处的切线垂直于 轴.
轴.
(1)求实数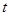 的值;
的值;
(2)求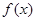 的极值.
的极值.
预算用2000元购买单件为50元的桌子和20元的椅子,希望使桌椅的总数尽可能的多,但椅子不少于桌子数,且不多于桌子数的1
 5倍,问桌、椅各买多少才行?
5倍,问桌、椅各买多少才行?
已知圆心为C的圆经过点A(1,1)和B(2,-2),且圆心C在直线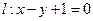 上,求圆心为C的圆的方程。
上,求圆心为C的圆的方程。
求经过直线L1:3x + 4y – 5 = 0与直线L2:2x – 3y + 8 = 0的交点M,且满足下列条件的直线方程:(1)与直线2x + y + 5 = 0平行;(2)与直线2x + y + 5 = 0垂直。
设 分别是椭圆C:
分别是椭圆C: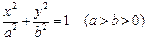 的左右焦点,
的左右焦点,
(1)设椭圆C上的点 到
到 两点距离之和等于4,写出椭圆C的方程和焦点坐标。
两点距离之和等于4,写出椭圆C的方程和焦点坐标。
(2)设K是(1)中所得椭圆上的动点,求线段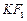 的中点B的轨迹方程。
的中点B的轨迹方程。
(3 )设点P是椭圆C 上的任意一点,过原点的直线L与椭圆相交于M,N两点,当直线PM ,PN的斜率都存在,并记为
)设点P是椭圆C 上的任意一点,过原点的直线L与椭圆相交于M,N两点,当直线PM ,PN的斜率都存在,并记为 试探究
试探究 的值是否与点P及直线L有关,并证明你的结论。
的值是否与点P及直线L有关,并证明你的结论。
(本题满分13分)
机床厂今年年初用98万元购进一台数控机床,并立即投入生产使用,计划第一年维修、保养费用12万元,从第二年开始,每年所需维修、保养费用比上一年增加4万元,该机床使用后,每年的总收入为50万元,设使用x年后数控机床的盈利额为y万元.
(1)写出y与x之间的函数关系式;
(2)从第几年开始,该机床开始盈利(盈利额为正值);
(3)使用若干年后,对机床的处理方案有两种:
(Ⅰ)当年平均盈利额达到最大值时,以30万元价格处理该机床;
(Ⅱ)当盈利额达到最大值时,以12万元价格处理该机床.
请你研究一下哪种方案处理较为合理?请说明理由.