已知抛物线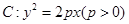 的焦点
的焦点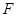 到准线的距离为
到准线的距离为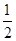 .过点
.过点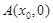
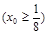
作直线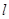 交抛物线
交抛物线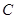 与
与 两点(
两点(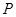 在第一象限内).
在第一象限内).
(1)若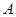 与焦点
与焦点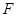 重合,且
重合,且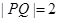 .求直线
.求直线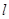 的方程;
的方程;
(2)设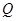 关于
关于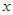 轴的对称点为
轴的对称点为 .直线
.直线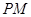 交
交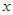 轴于
轴于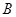 . 且
. 且 .求点
.求点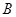 到直线
到直线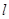 的距离的取值范围.
的距离的取值范围.
(本小题满分12分)已知数列{an},{bn}满足:a1b1+a2b2+a3b3+…+anbn=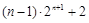 (
( ).
).
(Ⅰ)若{bn }是首项为1,公比为2的等比数列,求数列{an}的前n项和Sn;
(Ⅱ)若{an}是等差数列,且an≠0,问:{bn}是否是等比数列?若是,求{an}和{bn}的通项公式;若不是,请说明理由.
(本小题满分12分)已知向量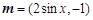 ,
,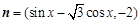 ,函数
,函数 .
.
(Ⅰ)求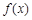 在区间
在区间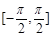 上的零点;
上的零点;
(Ⅱ)在△ABC中,角A,B,C的对边分别为a,b,c, 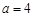 ,△ABC的面积
,△ABC的面积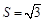 ,当x=A时,函数
,当x=A时,函数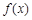 取得极大值,求
取得极大值,求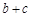 的值.
的值.
(本小题满分10分)选修4-5:不等式选讲
已知函数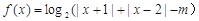 .
.
(Ⅰ)当 时,求函数
时,求函数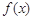 的定义域;
的定义域;
(Ⅱ)若关于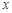 的不等式
的不等式 的解集是
的解集是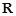 ,求
,求 的取值范围.
的取值范围.
(本小题满分10分)选修4-4:坐标系与参数方程
在平面直角坐标系中,以原点为极点,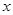 轴的正半轴为极轴建立极坐标系,两种坐标系取相同的单位长度. 已知曲线
轴的正半轴为极轴建立极坐标系,两种坐标系取相同的单位长度. 已知曲线
 ,过点
,过点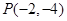 的直线
的直线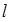 的参数方程为
的参数方程为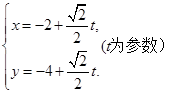 .直线
.直线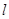 与曲线
与曲线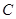 分别交于
分别交于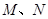 .
.
(Ⅰ)求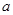 的取值范围;
的取值范围;
(Ⅱ)若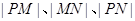 成等比数列,求实数
成等比数列,求实数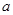 的值.
的值.
(本小题满分10分)选修4-1:几何证明选讲
如图,已知 是⊙
是⊙ 的直径,
的直径, 是⊙
是⊙ 的弦,
的弦,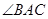 的平分线
的平分线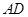 交⊙
交⊙ 于
于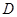 ,过点
,过点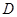 作
作 交
交 的延长线于点
的延长线于点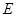 ,
,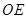 交
交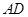 于点
于点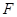 .若
.若 .
.
(Ⅰ)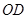 ∥
∥ ;
;
(Ⅱ)求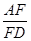 的值.
的值.