如图①,在矩形 ABCD中,AB=10cm,BC=8cm.点P从A出发,沿A→B→C→D路线运动,到D停止;点Q从D出发,沿 D→C→B→A路线运动,到A停止.若点P、点Q同时出发,点P的速度为每秒1cm,点Q的速度为每秒2cm,a秒时点P、点Q同时改变速度,点P的速度变为每秒bcm,点Q的速度变为每秒dcm.图②是点P出发x秒后△APD的面积S1(cm2)与x(秒)的函数关系图象;图③是点Q出发x秒后△AQD的面积S2(cm2)与x(秒)的函数关系图象.
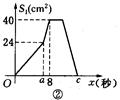

(1)参照图象,求b、图②中c及d的值;
(2)连接PQ,当PQ平分矩形ABCD的面积时,运动时间x的值为 ;
(3)当两点改变速度后,设点P、Q在运动线路上相距的路程为y(cm),求y(cm)与运动时间x(秒)之间的函数关系式,并写出自变量x的取值范围;
(4)若点P、点Q在运动路线上相距的路程为25cm,求x的值.
如图,AB是☉O的直径,AM和BN是☉O的两条切线,E是☉O上一点,D是AM上一点,连接DE并延长交BN于点C,且OD∥BE,OF∥BN. 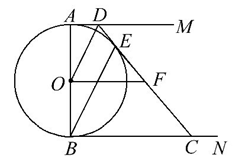
(1)求证:DE是☉O的切线.
(2)求证:OF =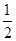 CD.
CD.
小丽和小华想利用摸球游戏决定谁去参加市里举办的书法比赛,游戏规则是:在一个不透明的袋子里装有除数字外完全相同的4个小球,上面分别标有数字2,3,4,5.一人先从袋中随机摸出一个小球,另一人再从袋中剩下的3个小球中随机摸出一个小球.若摸出的两个小球上的数字和为偶数,则小丽去参赛;否则小华去参赛.
(1)用列表法或画树状图法,求小丽参赛的概率.
(2)你认为这个游戏公平吗?请说明理由.
如图在▱ABCD中,EF∥AB,FG∥ED,DE∶EA=2∶3,EF=4,求线段CG的长.
如图,直线y=x+m和抛物线y=x2+bx+c都经过点A(1,0),B(3,2).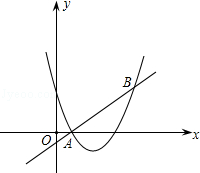
(1)求m的值和抛物线的解析式;
(2)求不等式x2+bx+c>x+m的解集.(直接写出答案)
△ABC在如图的平面直角坐标系中
(1)按要求画图:将△ABC向右平移3个单位长度后得△A1B1C1,再将△A1B1C1绕点O旋转180°后得到△A2B2C2.
(2)直接写出三角形A1A2B的面积.