已知数列 的通项
的通项 则
则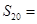 ().
().
| A.2246 | B.2148 | C.2146 | D.2248 |
已知某几何体的三视图如图所示(单位: ),其中正视图、侧视图都是等腰直角三角形,则这个几何体的体积是()
),其中正视图、侧视图都是等腰直角三角形,则这个几何体的体积是()
A. |
B.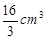 |
C.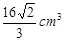 |
D. |

已知函数 ,则
,则 是().
是().
A.最小正周期为 的奇函数 的奇函数 |
B.最小正周期为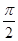 的奇函数 的奇函数 |
C.最小正周期为 的偶函数 的偶函数 |
D.最小正周期为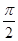 的偶函数 的偶函数 |
下面是某赛季甲、乙两名篮球运动员每场比赛得分的茎叶图,则甲、乙两人这几场比赛得分的中位数之和是 ( )
| A.62 | B.63 | C.64 | D.65 |
下列有关命题的说法正确的是 ( ).
A.命题“若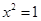 ,则 ,则 ”的否命题为:“若 ”的否命题为:“若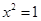 ,则 ,则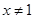 ”. ”. |
B.“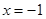 ”是“ ”是“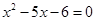 ”的必要不充分条件. ”的必要不充分条件. |
C.命题“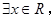 使得 使得 ”的否定是:“ ”的否定是:“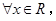 均有 均有 ”. ”. |
D.命题“若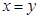 ,则 ,则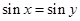 ”的逆否命题为真命题 ”的逆否命题为真命题 |