用数学归纳法证明“n3+(n+1)3+(n+2)3(n∈N*)能被9整除”,要利用归纳假设证n=k+1时的情况,只需展开( )
| A.(k+3)3 | B.(k+2)3 |
| C.(k+1)3 | D.(k+1)3+(k+2)3 |
已知a 平面
平面 ,点P
,点P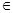
 ,那么过点P且平行于直线a的直线()
,那么过点P且平行于直线a的直线()
A.只有一条,不在 内 内 |
B.有无数条,不一定在 内 内 |
C.只有一条,且在 内 内 |
D.有无数条,一定在 内 内 |
已知平面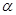 ,
,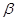 ,直线a,b,给出以下命题,正确的是()
,直线a,b,给出以下命题,正确的是()
A.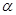 内有无穷多条直线都与 内有无穷多条直线都与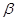 平行,则 平行,则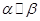 |
B.直线 ,且a不在 ,且a不在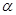 内也不在 内也不在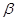 内,则 内,则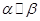 |
C.直线 ,则 ,则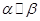 |
D.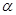 内任何直线都和 内任何直线都和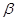 平行,则 平行,则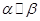 |
如图,正方体ABCD-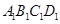 中, AB的中点为M,D
中, AB的中点为M,D 的中点为N,则异面直线
的中点为N,则异面直线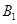 M与CN所成的角是()
M与CN所成的角是()
| A.0 | B.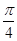 |
C.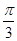 |
D.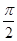 |
下列命题中正确的是()
A.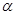 , ,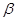 是两个相交的平面, 是两个相交的平面,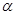 内存在两条相交直线都平行于 内存在两条相交直线都平行于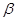 |
| B.两个不同的平面存在三个不共线的公共点 |
| C.经过一直线与一点有唯一一个平面 |
| D.经过平面外一点的直线一定在平面外。 |
 ,
,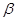 是两个不重合的平面,在下列条件中,可以判断
是两个不重合的平面,在下列条件中,可以判断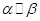 的是()
的是()
A.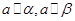 . . |
B. 有三个不共线的点到 有三个不共线的点到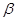 的距离相等 的距离相等 |
C. |
D. 为异面直线且 为异面直线且 |