(本小题满分12分) 设△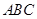 的内角
的内角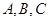 所对的边分别为
所对的边分别为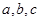 ,已知
,已知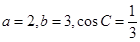 .
.
(1)求△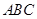 的面积;
的面积;
(2)求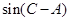 的值.
的值.
已知函数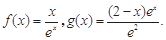
(1) 求函数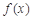 的极值;
的极值;
(2)求证:当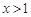 时,
时,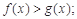
(3)如果 ,且
,且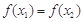 ,求证:
,求证: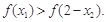
已知函数f(x)=cos(-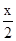 )+cos(
)+cos( ),k∈Z,x∈R.
),k∈Z,x∈R.
(1)求f(x)的最小正周期;
(2)求f(x)在[0,π)上的减区间;
(3)若f(α)= ,α∈(0,
,α∈(0,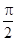 ),求tan(2α+
),求tan(2α+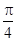 )的值.
)的值.
在△ABC中,角A、B、C所对的边分别为a、b、c,向量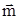 =
=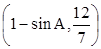 ,
, =(cos2A,2sinA),且
=(cos2A,2sinA),且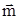 ∥
∥ .
.
(1)求sinA的值;
(2)若b=2,△ABC的面积为3,求a.
等比数列 中,
中,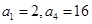 .
.
(1)求数列 的通项公式;
的通项公式;
(2)若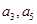 分别为等差数列
分别为等差数列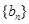 的第4项和第16项,求数列
的第4项和第16项,求数列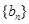 的前
的前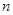 项和
项和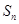 .
.