万有引力定律揭示了天体运动的规律与地上物体运动规律具有内在的一致性。
（1）用弹簧秤称量一个相对于地球静止的小物体的重量，随称量位置的变化可能会有不同的结果。已知地球的质量为，自转周期为，引力常量为。将地球看作是半径为，质量均匀分布的球体，不考虑空气的影响。设在地球北极地面称量时，弹簧秤的读数。
a.若在北极上空处称量，弹簧秤的读数为，求比值的表达式（并就的情形算出具体数值，（计算结果保留两位有效数字）
b.若在赤道地面处称量，弹簧秤的读数为，求比值的表达式
（2）设想地球绕太阳公转的半径为，太阳的半径为，地球的半径为，三者均减小为现在的1.0%，太阳和地球的密度均匀且不变，仅考虑太阳和地球之间的相互作用，以现实地球的1年为标准，计算"设想地球"的一年将变为多长？
如图甲所示，空间存在B=0.5T、方向竖直向下的匀强磁场，MN、PQ是相互平行的粗糙的长直导轨，处于同一水平面内，其间距L=0.2m，R是连在导轨一端的电阻，ab是跨接在导轨上质量m=0.1kg的导体棒，从零时刻开始，通过一小型电动机对ab棒施加一个牵引力F，方向水平向左，使其从静止开始沿导轨做加速运动，此过程中棒始终保持与导轨垂直且接触良好，图乙是棒的速度—时间图像，其中OA段是直线，AC是曲线，DE是曲线图像的渐近线，小型电动机功率在12s末达到额定功率Pm=4.5W，此后功率保持不变，除R以外，其余部分的电阻均不计，取g=10m/s2。求：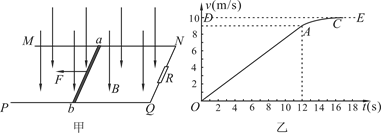
（1）导体棒在0～12s内的加速度大小；
（2）导体棒与导轨间的动摩擦因数和电阻R的阻值；
（3）若已知0～12s内R上产生的热量为12.5J，则此过程中牵引力F做的功。
如图所示的直角坐标系xOy中，x<0，y>0的区域内有沿x轴正方向的匀强电场，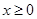
的区域内有垂直于xOy坐标平面向外的匀强磁场，x轴上P点坐标为（-L，0），y轴上M点的坐标为（0，
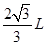）。有一个带正电的粒子从P点以初速度v沿y轴正方向射入匀强电场区域，经过M点进入匀强磁场区域，然后经x轴上的C点（图中未画出）运动到坐标原点O。不计重力。求：
（1）粒子在M点的速度v′；
（2）C点与O点的距离xc；
（3）匀强电场的电场强度E与匀强磁场的磁感应强度B的比值。
如图所示，一质量为m、电荷量为q的带负电的粒子，从A点射入宽度为d、磁感应强度为B的匀强磁场，MN、PQ为该磁场的边界线，磁场方向垂直于纸面向里，带电粒子射入时的初速度方向与下边界成θ=45°，且粒子恰好没有从MN边界射出，不计粒子所受重力，求该带电粒子初速度v0。
如图所示，质量为m1的物体甲通过三段轻绳悬挂，三段轻绳的结点为O，轻绳OB水平且B端与放置在水平面上的质量为m2的物体乙相连，轻绳OA与竖直方向的夹角θ=37°，物体甲、乙均处于静止状态。（已知sin37°=0.6，cos37°=0.8，tan37°=0.75，g取10m/s2.设最大静摩擦力等于滑动摩擦力）求：
（1）轻绳OA、OB受到的拉力是多大？
（2）物体乙受到的摩擦力是多大？方向如何？
（3）若物体乙的质量m2=4kg，物体乙与水平面之间的动摩擦因数为
=0.3，则欲使物体乙在水平面上不滑动，物体甲的质量m1最大不能超过多少？
跳伞运动员做低空跳伞表演，他离开飞机后先做自由落体运动，当距离地面125m时打开降落伞，伞张开后运动员就以14.3m/s2的加速度做匀减速运动，到达地面时速度为5m/s。（取g=10m/s2）
问：（1）运动员离开飞机时距地面的高度为多少？
（2）离开飞机后，经过多少时间才能到达地面？