如图所示，在无限长的竖直边界NS和MT间充满匀强电场，同时该-优题课

题文

如图所示，在无限长的竖直边界 $N S$ 和 $M T$ 间充满匀强电场，同时该区域上、下部分分别充满方向垂直于 $N S$ $T M$ 平面向外和 $B$ 和 $2 B$ ， $K L$ 为上下磁场的水平分界线，在 $N S$ 和 $M T$ 边界上，距 $K L$ 高 $h$ 处分别有 $P, Q$ 两点， $N S$ 和 $M T$ 间距为 $1.8 h$ .质量为 $m$ 、带电量为 $+ q$ 的粒子从 $P$ 点垂直于 $N S$ 边界射入该区域，在两边界之间做圆周运动，重力加速度为 $g$ .

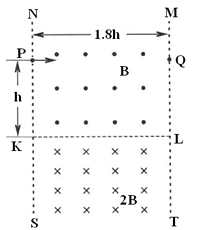
（1）求该电场强度的大小和方向。
（2）要使粒子不从 $N S$ 边界飞出，求粒子入射速度的最小值。
（3）若粒子能经过 $Q$ 点从 $M T$ 边界飞出，求粒子入射速度的所有可能值。

科目物理题型计算题难度较难

登录免费查看答案和解析

相关试题

有一个单摆、其摆长l=1.02m，摆球质量m=0.10kg，从与竖直方向成= 40的位置无初速度开始运动，已知振动的次数n=30次，用了时间t=60.8s，问：（取sin40=0.0698，cos40="0.9976," =3.14）
（1）重力加速度g为多大？
（2）摆球的最大回复力为多大？
（3）如果将这一单摆改成秒摆，摆长应怎样改变？

如图所示，在磁感应强度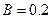T的水平匀强磁场中，有一边长为L=10cm，匝数N=100匝，电阻r=1Ω的正方形线圈绕垂直于磁感线的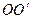轴匀速转动，转速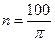r/s，有一电阻R=9Ω，通过电刷与两滑环接触，R两端接有一理想电压表，求：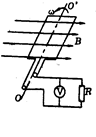

（1）若从线圈通过中性面时开始计时，写出电动势的表达式．
（2）电压表的示数．
（3）在1分钟内外力驱动线圈转动所作的功．

一列简谐横波在x轴上传播，在t1=0和t2=0.05s时刻，其波形图分别如图中的实线和虚线所示，求：（1）这列波可能具有的波速？（2）当波速为280m/s时，波的传播方向？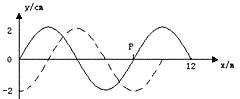

如图10所示，三块木板A、B、C的质量均为，长度均为L。A、B置于水平地面上，它们的间距s=2m。C置于B板的上端并对齐。A、B、C之间及A、B与地面之间的动摩擦因数均为μ=0．2，最大静摩擦力可以认为等于滑动摩擦力。开始时，三个物体处于静止状态。现给A施加一个水平向右，大小为的恒力F，假定木板A、B碰撞时间极短且碰撞后粘连在一起，最终C没有脱离A板，g取l0m／s2。求：

（1）碰撞后的瞬间A、B、C的速度各是多少?
（2）最终A、B、C的速度又是多少?
（3）要使C完全离开B并不脱离木板A，每块木板的长度应满足什么条件?[

如图9所示，在xOy平面的第二象限有一匀强电场，电场的方向沿轴方向；在y轴和第一象限的射线OC之间有一匀强磁场，磁感应强度的大小为B，方向垂直于纸面向外。有一质量为m，带有电荷量+q的质点由轴上的P点向平行于轴射人电场。质点到达y轴上A点时，速度方向与轴的夹角为，A点与原点0的距离为d。接着，质点进入磁场，并垂直于OC飞离磁场。不计重力影响。若OC与轴的夹角为，求：

（1）粒子在磁场中运动速度的大小；
（2）匀强电场P、A两点间的电势差．

试卷网试题网古诗词网作文网范文网