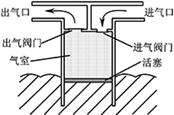
一种海浪发电机的气室如图所示。工作时，活塞随海浪上升或下降，改变气室中空气的压强，从而驱动进气阀门和出气阀门打开或关闭。气室先后经历吸入、压缩和排出空气的过程，推动出气口处的装置发电。气室中的空气可视为理想气体。
（1）下列对理想气体的理解，正确的有。
| A． | 理想气体实际上并不存在，只是一种理想模型 |
| B． | 只要气体压强不是很高就可视为理想气体 |
| C． | 一定质量的某种理想气体的内能与温度、体积都有关 |
| D． | 在任何温度、任何压强下，理想气体都遵循气体实验定律 |
（2）压缩过程中，两个阀门均关闭。若此过程中，气室中的气体与外界无热量交换，内能增加了3.4×104，则该气体的分子平均动能（选填"增大"、"减小"或"不变"），活塞对该气体所做的功（选填"大于"、"小于"或"等于"）3.4×104。
（3）上述过程中，气体刚被压缩时的温度为27℃，体积为0.2243，压强为1个标准大气压。已知1气体在1个标准大气压、0℃时的体积为22.4，阿伏加德罗常数＝6.02×1023－1。计算此时气室中气体的分子数。（计算结果保留一位有效数字）
如图所示,在矩形区域abcd内充满垂直纸面向里的匀强磁场,磁感应强度为B,在ad边中点的粒子源，在t=0时刻垂直于磁场发射出大量的同种带电粒子，所有粒子的初速度大小相同，方向与od的夹角分布在0~180°范围内。已知沿od方向发射的粒子在t=t0时刻刚好从磁场边界cd上的p点离开磁场，ab=1.5L，bc=
L，粒子在磁场中做圆周运动的半径R=L，不计粒子的重力和粒子间的相互作用，求：
(1)粒子在磁场中的运动周期T和粒子的比荷q/m；
(2)粒子在磁场中运动的最长时间；
(3)t=t0时刻仍在磁场中的粒子所处位置在某一圆弧上，在图中画出该圆弧并说明圆弧的圆心位置以及圆心角大小；
如图甲所示，在一对平行光滑的金属导轨的上端连接一阻值为R=4Ω的定值电阻，两导轨在同一平面内，质量为m=0.2kg，长为L=1.0m的导体棒ab垂直于导轨，使其从靠近电阻处由静止开始下滑，已知导体棒电阻为r=1Ω，整个装置处于垂直于导轨平面向上的匀强磁场中，导体棒下滑过程中加速度a与速度v的关系如图乙所示．求：
（1）导轨平面与水平面间夹角θ
（2）磁场的磁感应强度B；
（3）若靠近电阻处到底端距离为S=7.5m，ab棒在下滑至底端前速度已达5m/s，求ab棒下滑到底端的整个过程中，电阻R上产生的焦耳热．
如图所示是一个模拟风洞中的实验，空气压缩机在风洞可形成竖直向上的均匀气流。将一质量m=2kg的圆球套在与水平面成37°角的细直杆上，直杆固定不动，球内壁与杆间动摩擦因数μ=0.5，将此装置置于风洞中，气流可对球施加竖直向上的恒力F，某时刻由静止释放小球，经t=1s，小球通过的位移为S=0.5m．取g=10m/s2，sin37°=0.6，cos37°=0.8。
（1）求小球运动的加速度大小；
（2）求恒力F的大小；
（3）求运动1s内，小球机械能的变化量ΔE；
如图是过山车的部分模型图．模型图中光滑圆形轨道的半径R=8.1m，该光滑圆形轨道固定在倾角为α=37°斜轨道面上的Q点，圆形轨道的最高点A与P点平齐，圆形轨道与斜轨道之间圆滑连接．现使小车（视作质点）从P点以一定的初速度沿斜面向下运动，已知斜轨道面与小车间的动摩擦因数为μ=10/81，不计空气阻力，取g=10m/s2．sin37°=0.6，cos37°=0.8．若小车恰好能通过圆形轨道的最高点A处，问：
（1）小车在A点的速度为多大？
（2）小车在圆形轨道的最低点B时对轨道的压力为重力的多少倍？
（3）小车在P点的初速度为多大？
如图所示的区域中，左边为垂直纸面向里的匀强磁场，磁感应强度为 B ，右边是一个电场强度大小未知的匀强电场，其方向平行于OC且垂直于磁场方向．一个质量为m 、电荷量为-q 的带电粒子从P孔以初速度v0沿垂直于磁场方向进人匀强磁场中，初速度方向与边界线的夹角θ＝600，粒子恰好从C孔垂直于OC射入匀强电场，最后打在Q点且OQ间距是OC间距的2倍，不计粒子的重力，求： 
（1）电场强度E的大小
（2）粒子从P运动到Q所用的时间 t
（3）粒子到达Q点时的动能EKQ