如图,已知六棱锥P-ABCDEF的底面是正六边形,PA⊥平面ABC,PA=2AB,则下列结论正确的是( )
| A.PB⊥AD |
| B.平面PAB⊥平面PBC |
| C.直线BC∥平面PAE |
| D.直线PD与平面ABC所成的角为45° |
非空集合 关于运算
关于运算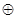 满足:(1)对任意
满足:(1)对任意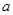 、
、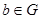 ,都有
,都有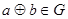 ;(2)存在
;(2)存在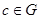 ,使得对一切
,使得对一切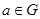 ,都有
,都有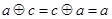 ,则称
,则称 关于运算
关于运算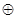 为“融洽集”。现给出下列集合和运算:
为“融洽集”。现给出下列集合和运算:
①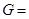 {非负整数},
{非负整数},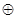 为整数的加法。
为整数的加法。
②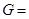 {偶数},
{偶数},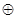 为整数的乘法。
为整数的乘法。
③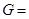 {平面向量},
{平面向量},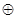 为平面向量的加法。
为平面向量的加法。
④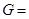 {二次三项式},
{二次三项式},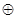 为多项式的加法。
为多项式的加法。
其中 关于运算
关于运算 为“融洽集”的是()
为“融洽集”的是()
| A.①② | B.①③ | C.②③ | D.②④ |
若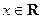 ,
,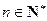 ,定义:
,定义: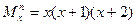
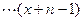 ,例如:
,例如: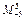 ="(-5)(-4)(-3)(-2)(-1)" =-120,则函数
="(-5)(-4)(-3)(-2)(-1)" =-120,则函数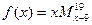 的奇偶性为()
的奇偶性为()
| A.是偶函数而不是奇函数 |
| B.是奇函数而不是偶函数 |
| C.既是奇函数又是偶函数 |
| D.既不是奇函数又不是偶函数 |
规定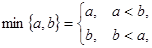 若函数
若函数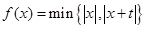 的图象关于直线
的图象关于直线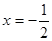 对称,则
对称,则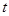 的值为()
的值为()
| A.-2 | B.2 | C.-1 | D.1 |
双曲线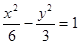 的渐近线与圆
的渐近线与圆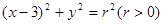 相切,则
相切,则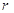 等于()
等于()
A.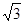 |
B.2 | C.3 | D.6 |
设奇函数 在
在 上为增函数,且
上为增函数,且 ,则不等式
,则不等式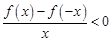 的解集为()
的解集为()
A.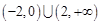 |
B. |
C. |
D. |