科学家在地球轨道外侧发现了一颗绕太阳运行的小行星,经过观测该小行星每隔t时间与地球相距最近,已知地球绕太阳公转的半径为R、公转周期为T,设地球和小行星运行轨道都是圆轨道,万有引力常量为G,由以上信息不能求出的物理量是
| A.小行星的质量 | B.太阳的质量 |
| C.小行星的公转周期 | D.小行星的公转轨道半径 |
匀强磁场中有一长方形闭合导线框,分别以相同的角速度绕图a、b、c、d所示的固定转轴旋转,用 、
、 、
、 、
、 表示四种情况下线框中电流的有效值,则()
表示四种情况下线框中电流的有效值,则()
A. |
B. |
C. |
D. |
如图甲所示,在粗糙的水平面上,质量分别为m和M的物块A、B用轻弹簧相连,两物块与水平面间的动摩擦因数相同,它们的质量之比m:M=1:2。当用水平力F作用于B上且两物块以相同的加速度向右加速运动时(如图甲所示),弹簧的伸长量为 ;当用同样大小的力F竖直向上拉B且两物块以相同的加速度竖直向上运动时(如图乙所示),弹簧的伸长量为
;当用同样大小的力F竖直向上拉B且两物块以相同的加速度竖直向上运动时(如图乙所示),弹簧的伸长量为 ,则
,则 等于()
等于()
A. 1 1 B. 1
1 B. 1 2 C. 2
2 C. 2 1 D. 2
1 D. 2 3
3
有一颗与地球同步静止轨道卫星在同一轨道平面的人造地球卫星,自西向东绕地球运行。已知它的运行半径为同步轨道半径的四分之一,地球自转周期为 ,则该卫星需要相隔多长时间才在赤道上同一城市的正上方再次出现()
,则该卫星需要相隔多长时间才在赤道上同一城市的正上方再次出现()
A. |
B. |
C. |
D. |
一列简谐横波沿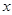 轴正方向传播,图甲是t=3s时的波形图,图乙是波中某质点P的振动图象(两图用同一时间起点),下列判断正确的是()
轴正方向传播,图甲是t=3s时的波形图,图乙是波中某质点P的振动图象(两图用同一时间起点),下列判断正确的是()
| A.质点P在t=3s时正向y轴负方向振动 |
| B.质点P在t=3s时的速度为零 |
C.质点P的平衡位置可能是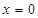 |
D.质点P的平衡位置可能是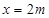 |
质量为1 kg的物体被人用手由静止向上提高1 m,这时物体的速度是2m/s,g取10m/s2,则下列说法中不正确的是()
| A.手对物体做功12J | B.合外力对物体做功12J |
| C.合外力对物体做功2J | D.物体克服重力做功10J |