如图所示，固定在水平地面上的工件，由AB和BD两部分组成，其中AB部分为光滑的圆弧，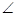
AOB=37o，圆弧的半径R=0．5m；BD部分水平，长度为0．2m，C为BD的中点。现有一质量m=lkg，可视为质点的物块从A端由静止释放，恰好能运动到D点。（g=10m/s2，sin37o=0．6，cos37o=0．8）求：
（1）物块运动到B点时，对工件的压力大小；
（2）为使物块恰好运动到C点静止，可以在物块运动到B点后，对它施加一竖直向下的恒力F，F应为多大?
（3）为使物块运动到C点时速度为零，也可先将BD部分以B为轴向上转动一锐角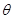
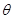，应为多大?（假设物块经过B点时没有能量损失）
如图所示，一辆汽车在平直公路上，车上有一木箱，试判断下列情况中，木箱所受摩擦力的方向.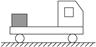
（1）汽车由静止加速运动时（木箱和汽车间无相对滑动）；
（2）汽车刹车时（二者无相对滑动）；
（3）汽车匀速运动时（二者无相对滑动）；
（4）汽车刹车，木箱在车上向前滑动时；
（5）汽车在匀速运动过程中突然加速，木箱在车上滑动时.
将G=50N的物体悬挂在轻质弹簧上,弹簧伸长了2.0cm, 静止时弹簧的弹力是多大?弹簧的劲度系数多大(如图甲)将弹簧从挂钩处摘下,在0点施加一个竖直向上的50N的拉力(图乙),物体仍然静止,那么弹簧的伸长量又是多少?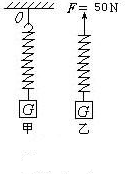
甲、乙两质点同时开始在彼此平行且靠近的两水平轨道上同向运动，甲在前，乙在后，相距s，甲初速度为零，加速度为a，做匀加速直线运动；乙以速度v0做匀速运动.关于两质点在相遇前的运动,
某同学作如下分析：设两质点相遇前，它们之间的距离为Δs，
则Δs=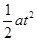
+s-v0t
当
时，两质点间距离Δs有最小值，也就是两质点速度相等时，两质点之间距离最近.
你觉得他的分析是否正确？如果认为是正确的，请求出它们的最小距离；如果认为是不正确的，请说明理由并作出正确分析.
一辆摩托车能达到的最大速度为vm＝30 m/s，要想在3 min内由静止起沿一条平直公路追上在前面s0＝1 000 m处、正以v＝20 m/s的速度匀速行驶的汽车，则摩托车至少以多大的加速度启动？（假设摩托车开始匀加速启动）以下是甲、乙两位同学的求解方法.
甲同学的解法是：设摩托车恰好在3 min时追上汽车，则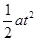
＝vt＋s0，代入数据得：a＝0.28 m/s2．
乙同学的解法是：设摩托车追上汽车时，摩托车的速度恰好是30 m/s，则
vm2＝2as＝2a（vt＋s0）,代入数据得：a＝0.1 m/s2．
你认为他们的解法正确吗？若都是错误的，请给出正确的解法.
《驾驶员守则》安全距离图中:具有良好刹车性能的汽车以80 km/h的速率行驶时,可以在60 m的距离内被刹住;在以40 km/h的速率行驶时,可以在20 m内的距离内被刹住.假设对于这两种速率,驾驶员所允许的反应时间与刹车的加速度都相同,则允许驾驶员的反应时间约为多少?