若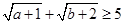 ,证明:
,证明: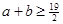
等比数列{an}中,a1,a2,a3分别是下表第一、二、三行中的某一个数,且a1,a2,a3中的任何两个数不在下表的同一列.
| 第一列 |
第二列 |
第三列 |
|
| 第一行 |
3 |
2 |
10 |
| 第二行 |
6 |
4 |
14 |
| 第三行 |
9 |
8 |
18 |
(1)求数列{an}的通项公式;
(2)若数列{bn}满足:bn=an+(-1)nlnan,求数列{bn}的前2n项和S2n.
已知等差数列{an}的前5项和为105,且a10=2a5.
(1)求数列{an}的通项公式;
(2)对任意m∈N*,将数列{an}中不大于72m的项的个数记为bm,求数列{bm}的前m项和Sm.
(1)已知两个等比数列{an},{bn},满足a1=a(a>0),b1-a1=1,b2-a2=2,b3-a3=3,若数列{an}唯一,求a的值;
(2)是否存在两个等比数列{an},{bn},使得b1-a1,b2-a2,b3-a3,b4-a4成公差不为0的等差数列?若存在,求{an},{bn}的通项公式;若不存在,说明理由.
设{an}是公比为正数的等比数列,a1=2,a3=a2+4,
(1)求{an}的通项公式;
(2)设{bn}是首项为1,公差为2的等差数列,求数列{an+bn}的前n项和Sn.
已知数列{an}的前n项和Sn=kcn-k(其中c,k为常数),且a2=4,a6=8a3.
(1)求an;
(2)求数列{nan}的前n项和Tn.