如图,半径为R的光滑半圆形轨道ABC在竖直平面内,与水平轨道CD相切于C 点,D端有一被锁定的轻质压缩弹簧,弹簧左端连接在固定的挡板上,弹簧右端Q到C点的距离为2R。质量为m的滑块(视为质点)从轨道上的P点由静止滑下,刚好能运动到Q点,并能触发弹簧解除锁定,然后滑块被弹回,且刚好能通过圆轨道的最高点A。已知∠POC=60°,求:
⑴滑块第一次滑至圆形轨道最低点C时对轨道压力;
⑵滑块与水平轨道间的动摩擦因数μ;
⑶弹簧被锁定时具有的弹性势能。
如图所示,质量0.1kg的小球.从光滑轨道顶端滚下,圆轨道半径R=0.5m.小球经过A和B时,速度分别为VA=4m/s和VB="8m/s" .设g=1 0m/s2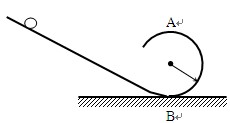
(1)计算小球在A时具有的重力势能(取B处为零势能)
(2)计算小球由B到达A时克服摩擦力所做的功
如图所示,用一根绝缘轻绳悬挂一个带电小球,小球的质量为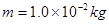 .现加一水平方向向左的匀强电场,场强
.现加一水平方向向左的匀强电场,场强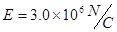 ,平衡时绝缘线与竖直方向的夹角为
,平衡时绝缘线与竖直方向的夹角为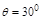 ,求:小球带何种电荷,电荷量为多大?
,求:小球带何种电荷,电荷量为多大?
如图所示,某人用滑板从圆弧形的竖直面某高度的A点滑至B点,接着沿水平路面滑至C点停止。若人与滑板的总质量为60kg。表中记录了开始下滑到停止过程中的有关数据,请根据图表中的数据求解下列问题:(取g=10m/s2)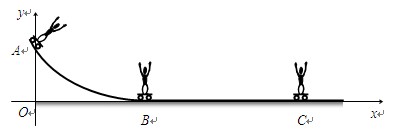
| 位置 |
A |
B |
C |
| 速度(m/s) |
0 |
8.0 |
0 |
| 位置坐标(m) |
(0,5) |
(10,0) |
(30,0) |
(1)人与滑板从A滑到B的过程中,损失的机械能为多少?
(2)若滑板在BC段所受阻力恒定,则阻力为多大?
将一测力传感器连接到计算机上就可以测量快速变化的力,图甲中O点为单摆的悬点,现将小球(可视为质点)拉到A点,此时细线处于张紧状态,释放摆球,则摆球在竖直平面内的ABC之间来回摆动,其中B点为运动中最低位置。∠AOB=∠COB=α,α小于10°且是未知量,图乙表示由计算机得到细线对摆球的拉力大小F随时间变化的曲线,且图中t=0时刻为摆球从A点开始运动的时刻,据力学规律和题中信息(g取10m/s2),求:
(1)单摆的周期和摆长; (2)摆球质量及摆动过程中的最大速度.
一束单色光由左侧射入盛有清水的薄壁圆柱形玻璃杯,如图为过轴线的截面图,调整入射角α,使光线恰好在水和空气的界面上发生全反射,已知水的折射率为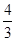 ,求sin α的值.
,求sin α的值.