我区某房地产开发公司于2013年5月份完工一商品房小区，6月初开始销售，其中6月的销售单价为0.7万元/m2，7月的销售单价为0.72万元/m2，且每月销售价格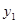
(单位：
)与月份x(6≤x≤11,x为整数)之间满足一次函数关系，每月的销售面积为
(单位：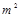
)，其中y2=-2000x+26000(6≤x≤11,x为整数)．
(1)求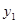与月份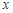
的函数关系式；
(2)6～11月中，哪一个月的销售额最高？最高销售额为多少万元？
(3)2013年11月时，因受某些因素影响，该公司销售部预计12月份的销售面积会在11月销售面积基础上减少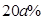
，于是决定将12月份的销售价格在11月的基础上增加
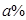，该计划顺利完成．为了尽快收回资金，2014年1月公司进行降价促销，该月销售额为(1500+600a)万元．这样12月、1月的销售额共为
万元，请根据以上条件求出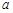
的值为多少？
解不等式组
并把解集在数轴上表示出来．
（1）计算：（）0 - （）-2 +
；
（2）解方程： - = 2．
如图，正方形纸片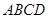
的边长为4，将其沿
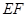折叠，则图中①②③④四个三角形的周长之和为.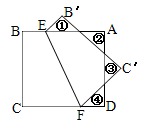
如图，已知抛物线y=ax2+bx+c（a≠0）经过A（﹣1，0），B（4，0），C（0，2）三点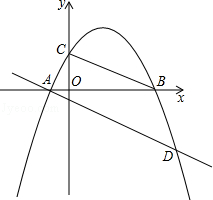
（1）求这条抛物线的解析式；
（2）E为抛物线上一动点，是否存在点E使以A、B、E为顶点的三角形与△COB相似？若存在，试求出点E的坐标；若不存在，请说明理由；
某企业设计了一款工艺品，每件的成本是50元，为了合理定价，投放市场进行试销．据市场调查，销售单价是100元时，每天的销售量是50件，而销售单价每降低1元，每天就可多售出5件，但要求销售单价不得低于成本．
求销售单价为多少元时，每天的销售利润最大？最大利润是多少？