已知函数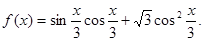
(1)将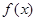 写成
写成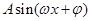 的形式,并求其图象对称中心的横坐标;
的形式,并求其图象对称中心的横坐标;
(2)如果△ABC的三边 满足
满足 ,且边
,且边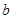 所对的角为
所对的角为 ,试求
,试求 的范围及此时函数
的范围及此时函数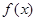 的值域.
的值域.
(本小题满分12分)为了降低能源损耗,某体育馆的外墙需要建造隔热层.体育馆要建造可使用20年的隔热层,每厘米厚的隔热层建造成本为6万元.该建筑物每年的能源消耗费用C万元与隔热层厚度 cm满足关系:
cm满足关系: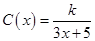 (
(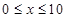 ,
,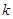 为常数),若不建隔热层,每年能源消耗费用为8万元.设
为常数),若不建隔热层,每年能源消耗费用为8万元.设 为隔热层建造费用与20年的能源消耗费用之和.
为隔热层建造费用与20年的能源消耗费用之和.
(Ⅰ)求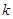 的值及
的值及 的表达式;
的表达式;
(Ⅱ)隔热层修建多厚时,总费用 达到最小?并求最小值.
达到最小?并求最小值.
(本小题满分12分)已知向量 ,
, ,函数
,函数 .
.
(Ⅰ)求函数 的对称中心;
的对称中心;
(Ⅱ)在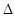
 中,
中,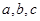 分别是角
分别是角 的对边,且
的对边,且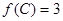 ,
, ,
,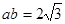 ,且
,且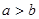 ,求
,求 的值.
的值.
(本小题满分10分)选修 :不等式选讲
:不等式选讲
已知函数 ,
,
(1)当 时,求不等式
时,求不等式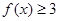 的解集;
的解集;
(2)若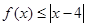 的解集包含
的解集包含 ,求
,求 的取值范围.
的取值范围.
(本小题满分10分)选修4-4:坐标系与参数方程
在直角坐标系xOy 中,曲线C1的参数方程为: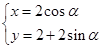 (
(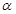 为参数),M是C1上的动点,P点满足
为参数),M是C1上的动点,P点满足 ,P点的轨迹为曲线C2.
,P点的轨迹为曲线C2.
(1)求C2的方程;
(2)在以O为极点,x 轴的正半轴为极轴的极坐标系中,射线 与C1的异于极点的交点为A,与C2的异于极点的交点为B,求
与C1的异于极点的交点为A,与C2的异于极点的交点为B,求 .
.
(本小题满分10分)选修4-1:几何证明选讲
如图,四边形ABCD是⊙O的内接四边形,AB的延长线与DC的延长线交于点E,且CB=CE.
(1)证明:∠D=∠E;
(2)设AD不是⊙O的直径,AD的中点为M,且MB=MC,证明:△ADE为等边三角形.