某毕业生参加人才招聘会，分别向甲、乙、丙三个公司投递了个人简-优题课

题文

某毕业生参加人才招聘会，分别向甲、乙、丙三个公司投递了个人简历．假定该毕业生得到甲公司面试的概率为，得到乙、丙两公司面试的概率均为p，且三个公司是否让其面试是相互独立的．记X为该毕业生得到面试的公司个数．若P(X＝0)＝，则随机变量X的数学期望E(X)＝________．

科目数学题型填空题难度较易

知识点：随机思想的发展

登录免费查看答案和解析

相关试题

下图是某学校一名篮球运动员在五场比赛中所得分数的茎叶图，则该运动员在这五场比赛中得分的方差为.

(注：方差 $s^{2} = \frac{1}{n} [{(x_{1} - \bar{x})}^{2} + {(x_{2} - \bar{x})}^{2} + \dots + {(x_{n} - \bar{x})}^{2}]$ ，其中 $\bar{x}$ 为 $x_{1}$ ， $x_{2}$ ，…， $x_{n}$ 的平均数)

不等式 $x^{2} - 5 x + 6 \leq 0$ 的解集为.

某制药企业为了对某种药用液体进行生物测定，需要优选培养温度，实验范围定为29 $℃$ $~$ 63 $℃$ .精确度要求±1 $℃$ .用分数法进行优选时，能保证找到最佳培养温度需要最少实验次数为.

在极坐标系中，曲线 $C_{1} : ρ (\sqrt{2} \cos θ + \sin θ) = 1$ 与曲线 $C_{2} : ρ = a (a > 0)$ 的一个交点在极轴上，则 $a =$ .

传说古希腊毕达哥拉斯学派的数学家经常在沙滩上面画点或用小石子表示数。他们研究过如图所示的三角形数：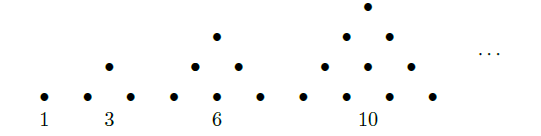

将三角形数1,3， 6,10，…记为数列 ${a_{n}}$ ，将可被5整除的三角形数按从小到大的顺序组成一个新数列 ${b_{n}}$ ，可以推测：
（Ⅰ） $b_{2012}$ 是数列 ${a_{n}}$ 中的第项；
（Ⅱ） $b_{2 k - 1} =$ .（用 $k$ 表示）

试卷网试题网古诗词网作文网范文网

Copyright ©2020-2025 优题课 youtike.com 版权所有

粤ICP备20024846号