已知椭圆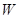 :
: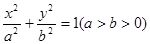 的短轴长为
的短轴长为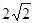 ,且斜率为
,且斜率为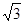 的直线
的直线 过椭圆
过椭圆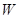 的焦点及点
的焦点及点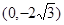 .
.
(1)求椭圆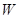 的方程;
的方程;
(2)已知直线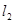 过椭圆
过椭圆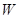 的左焦点
的左焦点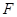 ,交椭圆于点P、Q.
,交椭圆于点P、Q.
(ⅰ)若满足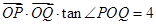 (
(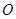 为坐标原点),求
为坐标原点),求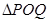 的面积;
的面积;
(ⅱ)若直线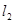 与两坐标轴都不垂直,点
与两坐标轴都不垂直,点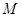 在
在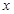 轴上,且使
轴上,且使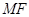 为
为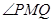 的一条角平分线,则称点
的一条角平分线,则称点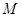 为椭圆
为椭圆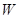 的“特征点”,求椭圆
的“特征点”,求椭圆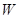 的特征点.
的特征点.
有一城市,市区为半径为15 km的圆形区域,近郊区为距中心15—25 km的范围内的环形地带,距中心25 km以外的为远郊区,如右图所示.市区地价每公顷100万元,近郊区地价每公顷60万元,远郊区地价为每公顷20万元,输入某一点的坐标为(x,y),求该点的地价. 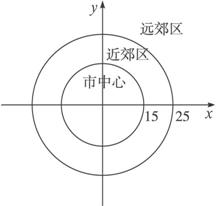
“特快专递”是目前人们经常使用的异地邮寄信函或托运物品的一种快捷方式.某快递公司规定甲、乙两地之间物品的托运费用根据下列方法计算:
f=
其中f(单位:元)为托运费,ω为托运物品的重量(单位:千克).
试画出计算费用f的程序框图.
设计算法,找出输入的三个不相等实数a、b、c中的最大值,并画出流程图.
设计算法,求ax+b=0的解,并画出流程图.
变换两个变量A和B的值,并输出交换前后的值.