在直角坐标系中,设x轴为直线l,函数 的图像分别是
的图像分别是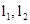 ,半径为1的
,半径为1的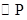 与直线
与直线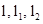 中的两条相切,例如
中的两条相切,例如 是其中一个
是其中一个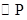 的圆心坐标.
的圆心坐标.
(1)写出其余满足条件的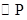 的圆心坐标;
的圆心坐标;
(2)在图中标出所有圆心,并用线段依次连接各圆心,求所得几何图形的周长.
在平面直角坐标系 中,抛物线
中,抛物线 的开口向下,且抛物线与
的开口向下,且抛物线与 轴的交于点
轴的交于点 ,与
,与 轴交于
轴交于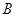 ,
, 两点,(
两点,(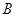 在
在 左侧). 点
左侧). 点 的纵坐标是
的纵坐标是 .
.
(1)求抛物线的解析式;
(2)求直线 的解析式;
的解析式;
(3)将抛物线在点 左侧的图形(含点
左侧的图形(含点 )记为
)记为 .若直线
.若直线 与直线
与直线 平行,且与
平行,且与
图形 恰有一个公共点,结合函数图象写出
恰有一个公共点,结合函数图象写出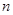 的取值范围.
的取值范围.
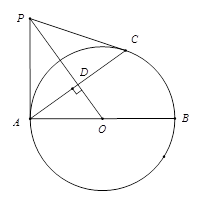
如图,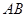 是
是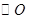 的直径,
的直径,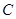 是圆周上一点,
是圆周上一点,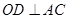 于点
于点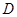 .
.
过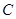 作
作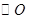 的切线,交
的切线,交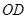 的延长线于点
的延长线于点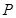 ,连接
,连接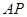 .
.
(1)求证: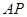 是
是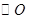 的切线.
的切线.
(2)若 ,
,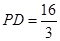 ,求
,求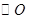 的半径.
的半径.
在 中,
中,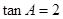 ,
,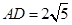 ,
, ,
, 是
是 中点,
中点, 于
于 .
.
(1)求 的度数.
的度数.
(2)求四边形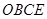 的面积.
的面积.
在平面直角坐标系 中,一次函数
中,一次函数 和函数
和函数 都经过
都经过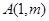 .
.
(1)求 值和一次函数的解析式;
值和一次函数的解析式;
(2)点 在函数
在函数 的图象上,且位于直线
的图象上,且位于直线 下方.若点
下方.若点 的横纵坐标都为整数,直接写出点
的横纵坐标都为整数,直接写出点 的坐标.
的坐标.
如图,某数学兴趣小组想测量一棵树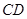 的高度,他们先在点
的高度,他们先在点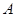 处测得树顶
处测得树顶 的仰角为
的仰角为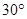 ,然后沿
,然后沿 方向前行
方向前行 ,到达
,到达 点,在
点,在 处测得树顶
处测得树顶 的仰角高度为
的仰角高度为 (
(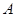 、
、 、
、 三点在同一直线上).请你根据他们测量数据计算这棵树
三点在同一直线上).请你根据他们测量数据计算这棵树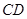 的高度(结果精确到
的高度(结果精确到 ).(参考数据:
).(参考数据: ≈1.732)
≈1.732)