能的转化与守恒是自然界普遍存在的规律，如：电源给电容器的充电过程可以等效为将电荷逐个从原本电中性的两极板中的一个极板移到另一个极板的过程. 在移动过程中克服电场力做功，电源的电能转化为电容器的电场能．实验表明:电容器两极间的电压与电容器所带电量如图所示．
（1）对于直线运动，教科书中讲解了由v-t图像求位移的方法．请你借鉴此方法，根据图示的Q-U图像，若电容器电容为C，两极板间电压为U，证明：电容器所储存的电场能为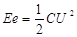
．
（2）如图所示，平行金属框架竖直放置在绝缘地面上．框架上端接有一电容为C的电容器．框架上一质量为m、长为L的金属棒平行于地面放置，离地面的高度为h．磁感应强度为B的匀强磁场与框架平面相垂直．现将金属棒由静止开始释放，金属棒下滑过程中与框架接触良好且无摩擦．开始时电容器不带电，不计各处电阻．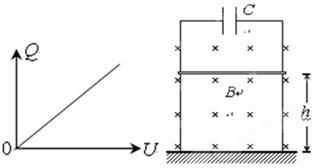
求：a. 金属棒落地时的速度大小 b. 金属棒从静止释放到落到地面的时间
如图所示，一横截面为半圆柱形的透明物体，底面AOB镀银（图中粗线），O表示半圆截面的圆心，一束光线在横截面内从M点的入射角为30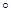
，
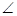MOA=60，NOB=30。
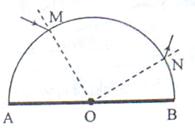
求（1）作出光路图，并求光线在M点的折射角；
（2）透明物体的折射率。
一列简谐横波沿x轴负向传播，t＝0时刻的波形如图所示，介质中质点P、Q分别位于x＝2m、x＝4m处。从t＝0时刻开始计时，当t＝26s时质点Q第4次到达波峰。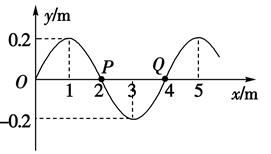
（1）求波速。
（2）写出质点P做简谐运动的表达式(不要求推导过程)。
如图所示，ABC是三棱镜的一个截面，其折射率为n＝1.5，现有一细束平行于截面的光线沿MN方向射到棱镜的AB面上的N点，AN＝NB＝2cm，入射角的大小为i，且sini＝0.75。已知真空中的光速c＝3.0×108 m/s，求：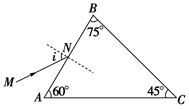
(1)光在棱镜中传播的速率；
(2)此束光进入棱镜后从棱镜射出的方向和位置。(不考虑AB面的反射)
一束细光束由真空沿着径向射入一块半圆柱形透明体，如图(a)所示，对其射出后的折射光线的强度进行记录，发现折射光线的强度随着θ的变化而变化，如图(b)的图线所示，求此透明体的临界角和折射率。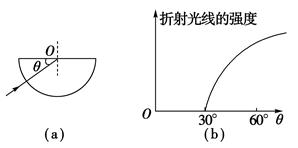
如图甲是一个单摆振动的情形，O是它的平衡位置，B、C是摆球所能到达的最远位置．
设摆球向右运动为正方向．图乙是这个单摆的振动图象．根据图象回答：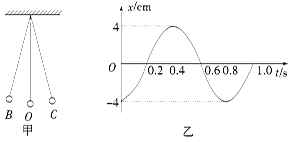
(1)单摆振动的频率是多大？
(2)开始时刻摆球在何位置？
(3)若当地的重力加速度为10 m/s2，这个摆的摆长是多少？