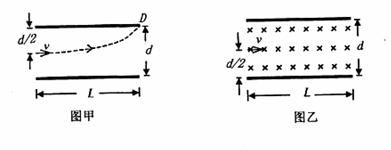地球的质量M=5.98×1024kg,地球半径R=6370km,引力常量G=6.67×10-11N·m2/kg2,一颗绕地做圆周运动的卫星环绕速度为v=2100m/s,求:
(1)用题中的已知量表示此卫星距地面高度h的表达式
(2)此高度的数值为多少?(保留3位有效数字)
如图13所示,在平面直角坐标系 中,仅在第Ⅱ象限存在沿
中,仅在第Ⅱ象限存在沿 轴正方向的匀强电场,一质量为
轴正方向的匀强电场,一质量为 ,电荷量为
,电荷量为 ,可视为质点的带正电粒子(重力不计)从
,可视为质点的带正电粒子(重力不计)从 轴负半轴
轴负半轴 处的M点,以初速度
处的M点,以初速度 垂直于
垂直于 轴射入电场,经
轴射入电场,经 轴上
轴上 处的P点进入第I象限。
处的P点进入第I象限。
(1)求电场强度的大小和粒子进入第I象限的速度大小。
(2)现要在第I象限内加一半轻适当的半圆形匀强磁场区域,使(1)问中进入第I象限的粒子,恰好以垂直于 轴的方
轴的方 向射出磁场。求所知磁场区域的半径。要求;磁场区域的边界过坐标原点,圆心在
向射出磁场。求所知磁场区域的半径。要求;磁场区域的边界过坐标原点,圆心在 一上,磁场方向垂直于从标平面向外,磁感应强度为
一上,磁场方向垂直于从标平面向外,磁感应强度为

如图12所示,A为一具有光滑曲面的固定轨道,轨道底端是水平的,质量M=40kg的上车B静止于轨道右侧,其板面与轨道底端靠近且在同一水平面上,一个质量m="20" kg,可视为质点的小滑块C以 的初速度从轨道顶端滑下,C冲上小车B后,经一段时间与小车相对静止并继续一起运动。若轨道顶端与底端水平面的高度差为
的初速度从轨道顶端滑下,C冲上小车B后,经一段时间与小车相对静止并继续一起运动。若轨道顶端与底端水平面的高度差为 ,C与小车板面间的动摩擦因数为
,C与小车板面间的动摩擦因数为 ,小车与水平面间的摩擦不计,
,小车与水平面间的摩擦不计, 取10m/s2。求
取10m/s2。求
(1)C与小车保持相对静止时的速度大小。
(2)从C冲上小车瞬间到与小车相对静止瞬间所用的时间。
(3)C冲上小车后相对于小车板面滑动的距离。
如图11所示,总质量为 ,可视为质点的滑雪运动员(包括装备
,可视为质点的滑雪运动员(包括装备 )从高为
)从高为 的斜面AB的顶端A点由静止开始沿斜面下滑,在B点进入四分之一圆弧轨道BC,圆弧半径R=5m,运动员在C点沿竖直方向冲出轨道,经过时间4s又从C点落回轨道。若运动员从C点离开轨道后受到的空气阻力不计,g取10m/s2。求:
的斜面AB的顶端A点由静止开始沿斜面下滑,在B点进入四分之一圆弧轨道BC,圆弧半径R=5m,运动员在C点沿竖直方向冲出轨道,经过时间4s又从C点落回轨道。若运动员从C点离开轨道后受到的空气阻力不计,g取10m/s2。求:
(1)运动员在C点处的速度大小。
(2)运动员从A到C的过程中损失的机械能。
某地地磁场的磁感应强度方向斜向下指向地面,与竖直方向成60°角,大小为5 ×10-5T。一灵敏电压表通过导线连接在当地入海河段的两岩的接线柱上,接线柱与水接触良好。已知该河段的两岸南北正对,河宽200m,该河段涨潮和落潮时有海水(视为导体、电阻极小)流过。设落潮时,海水自正西向正东流,流速为4m/s。
(1)该河段的南岸和北岸,那边电势高?
(2)灵敏电压表的示数是多少?
有一平行板电容器,内部为真空,两个电极板的间距为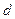 ,每一个正方形电极板的长均为L,电容器内有一均匀电场,U为两个电极板间的电压,如图甲所示。电子从电容器左端的正中央以初速
,每一个正方形电极板的长均为L,电容器内有一均匀电场,U为两个电极板间的电压,如图甲所示。电子从电容器左端的正中央以初速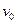 射入,其方向平行于电极板之一边,并打在图上的D点。电子的电荷以-e表示,质量以
射入,其方向平行于电极板之一边,并打在图上的D点。电子的电荷以-e表示,质量以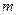 表示,重力可不计。回答下面各问题(用已知物理的字母表示)
表示,重力可不计。回答下面各问题(用已知物理的字母表示)
(1)求电子打到D点瞬间的动能;
(2)电子的初速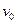 至少必须大于何值,电子才能避开电极板,逸出电容器外?
至少必须大于何值,电子才能避开电极板,逸出电容器外?
(3)若电容器内没有电场,只有垂直进入纸面的均匀磁场,其磁感应强度为B,电子从电容器左端的正中央以平行于电极板一边的初速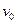 射入,如图乙所示,则电子的初速
射入,如图乙所示,则电子的初速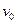 为何值,电子才能避开电极板,逸出电容器外?
为何值,电子才能避开电极板,逸出电容器外?