如图所示,半径为R的半球形陶罐,固定在可以绕竖直轴旋转的水平转台上,转台转轴与过陶罐球心O的对称轴OO′重合。转台以一定角速度ω匀速转动,一质量为m的小物块落入陶罐内,经过一段时间后,小物块随陶罐一起转动且相对罐壁静止,它和O点的连线与OO′之间的夹角θ为60°.重力加速度大小为g。若ω=ω0,小物块受到的摩擦力恰好为零,求ω0;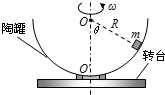
有一起重机用的直流电动机,如图所示,其内阻r=0.8Ω,线路电阻R=10Ω,电源电压U=150V,电压表示数为110V,求:(1)通过电动机的电流;(2)输入到电动机的功率P入;(3)电动机的发热功率Pr,电动机输出的机械功率.(4)若电动机被卡住不能转动,这时通过电动机的电流为多大?电动机消耗的电功率和发热功率又各是多少?
如图所示,两平行金属板A、B间为一匀强电场,A、B相距d=6cm,C、D为电场中的两点,且C、D 相距d1=4cm,CD连线和场强方向成60°角.已知电子从D点移到C点电场力做功为W=3.2×10-17J,求: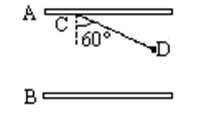
匀强电场的场强E;
A、B两点间的电势差UAB;
若A板接地,D点电势φD为多少?
两条相距为1m的水平金属导轨上放置一根导电棒ab,处于竖直方向的匀强磁场中,如图示,导电棒的质量是1.2kg,当棒中通入2安培的电流时(电流方向是从a到b),它可在导轨上向右匀速滑动,如电流增大到4A时,棒可获得0.5m/s2的加速度。求
磁场的方向?
磁场的磁感强度的大小和摩擦力大小
将长度为20cm、通有0.1A电流的直导线放入一匀强磁场中,电流与磁场的方向如图所示,已知磁感应强度为1T。试求出下列各图中导线所受安培力的大小和方向。(写图边)
(15分)如图所示,板A的质量为m,滑块B的质量为2m,板A用绳拴住,绳与斜面平行,滑块B沿倾角为α的斜面在A板的中间一段匀速下滑,若A、B之间以及B与斜面间的动摩擦因数相同,求动摩擦因数μ.