如图1，在△ABC中，E、D分别为AB、AC上的点，且ED//BC，O为DC中点，连结EO并延长交BC的延长线于点F，则有S四边形EBCD=S△EBF.
（1）如图2，在已知锐角∠AOB内有一个定点P．过点P任意作一条直线MN，分别交射线OA、OB于点M、N．将直线MN绕着点P旋转的过程中发现，当直线MN满足某个条件时，△MON的面积存在最小值．直接写出这个条件:_______________________.
（2）如图3，在平面直角坐标系中，O为坐标原点，点A、B、C、P的坐标分别为（6，0）、（6，3）、（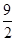
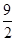，）、（4、2），过点P的直线l与四边形OABC一组对边相交，将四边形OABC分成两个四边形，求其中以点O为顶点的四边形面积的最大值．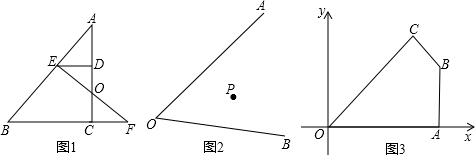
一个矩形周长为56厘米．
（1）当矩形面积为180平方厘米时，长宽分别为多少？
（2）能围成面积为200平方厘米的矩形吗？请说明理由．
深圳市某学校抽样调查， 
类学生骑共享单车， 
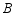类学生坐公交车、私家车等， 
类学生步行，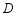 
类学生（其它），根据调查结果绘制了不完整的统计图．
|
类型 |
频数 |
频率 |
|
|
30 |
|
|
|
18 |
0.15 |
|
|
|
0.40 |
|
|
|
|
（1）学生共 人，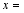 
， 
；
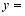（2）补全条形统计图；
（3）若该校共有2000人，骑共享单车的有 人．
先化简，再求值：
，其中 
．
计算： ．
如图，抛物线y＝ax2+bx﹣4（a≠0）与x轴交于A（4，0）、B（﹣1，0）两点，过点A的直线y＝﹣x+4交抛物线于点C．
（1）求此抛物线的解析式；
（2）在直线AC上有一动点E，当点E在某个位置时，使△BDE的周长最小，求此时E点坐标；
（3）当动点E在直线AC与抛物线围成的封闭线A→C→B→D→A上运动时，是否存在使△BDE为直角三角形的情况，若存在，请直接写出符合要求的E点的坐标；若不存在，请说明理由．
