现有10道题,其中6道甲类题,4道乙类题,张同学从中任取3道题解答.
(1)求张同学至少取到1道乙类题的概率;
(2)已知所取的3道题中有2道甲类题,1道乙类题.设张同学答对每道甲类题的概率都是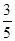 ,答对每道乙类题的概率都是
,答对每道乙类题的概率都是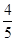 ,且各题答对与否相互独立.用
,且各题答对与否相互独立.用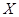 表示张同学答对题的个数,求
表示张同学答对题的个数,求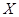 的分布列和数学期望.
的分布列和数学期望.
在数列{an}中, ,试猜想这个数列的通项公式。
,试猜想这个数列的通项公式。
对于区间 (或
(或 、
、 、
、 ),我们定义
),我们定义 为该区间的长度,特别地,
为该区间的长度,特别地, 和
和 的区间长度为正无穷大.
的区间长度为正无穷大.
(1)关于 的不等式
的不等式 的解集的区间长度不小于4,求实数
的解集的区间长度不小于4,求实数 的取值范围;
的取值范围;
(2)关于 的不等式
的不等式 恰好有3个整数解,求实数
恰好有3个整数解,求实数 的取值范围.
的取值范围.
已知{ }是等差数列,其前
}是等差数列,其前 项和为
项和为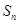 ,{
,{ }是等比数列,且
}是等比数列,且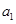 =
= ,
, ,
,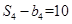 .
.
(1)求数列{ }与{
}与{ }的通项公式;
}的通项公式;
(2)记 ,求满足不等式
,求满足不等式 的最小正整数
的最小正整数 的值.
的值.
如图所示是某水产养殖厂的养殖大网箱的平面图,四周的实线为网衣,为避免混养,
(1)若大网箱的面积为108平方米,每个小网箱的横边 、纵边
、纵边 设计为多少米时,才能使围成的网箱中筛网的总长度最小?
设计为多少米时,才能使围成的网箱中筛网的总长度最小?
(2)若大网箱的面积为160平方米,网衣的造价为112元/米,筛网的造价为96元/米,且大网箱的长与宽都不超过15米,则小网箱的横、纵边分别为多少米时,可使总造价最低?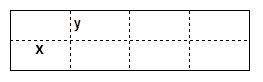
在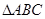 中,内角
中,内角 所对的分别是
所对的分别是 ,已知
,已知 ;
;
(I)求 和
和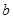 的值;(II)求
的值;(II)求 的值.
的值.