在某大学自主招生考试中，所有选报II类志向的考生全部参加了“数学与逻辑”和“阅读与表达”两个科目的考试，成绩分为A,B,C,D,E五个等级. 某考场考生两科的考试成绩的数据统计如下图所示，其中“数学与逻辑”科目的成绩为B的考生有10人. 
（1）求该考场考生中“阅读与表达”科目中成绩为A的人数；
（2）若等级A，B，C，D，E分别对应5分，4分，3分，2分，1分.
（i）求该考场考生“数学与逻辑”科目的平均分；
(ii)若该考场共有10人得分大于7分，其中有2人10分，2人9分， 6人8分. 从这10中随机抽取两人，求两人成绩之和大于等于18的概率.
（本题满分共15分）已知函数
（1）当
时，试判断函数
的单调性；
（2）当
时，对于任意的
，恒有
，求
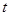的最大值．
（本题满分共15分）已知抛物线
的焦点F到直线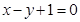
的距离为
．
（1）求抛物线的方程；
（2）如图，过点F作两条直线分别交抛物线于A、B和C、D，过点F作垂直于
轴的直线分别交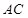
和
于点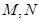
.
求证：
．
（本题满分共14分）已知数列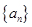
，
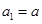，且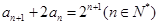
，
（1）若
成等差数列，求实数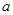
的值；（2）数列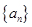能为等比数列吗？若能，
试写出它的充要条件并加以证明；若不能，请说明理由。
（本题满分共14分）已知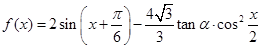
，
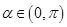且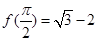
.
（1）求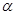
；
（2）当
时，求函数
的值域.
本题满分14分) 设函数f (x)＝ln x＋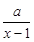
在(0，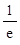
) 内有极值．
(Ⅰ) 求实数a的取值范围；
(Ⅱ) 若x1∈(0，1)，x2∈(1，＋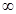
)．求证：f (x2)－f (x1)＞e＋2－．
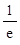注：e是自然对数的底数．