A、B两地相距1千米，B、C两地相距3千米，甲从A地出发，经过B前往C地，乙同时从B地出发，前往C地．甲、乙的速度关于时间的关系式分别为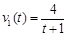
和
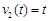（单位：千米/小时）．甲、乙从起点到终点的过程中，给出下列描述：
①出发后1小时，甲还没追上乙 ② 出发后1小时，甲乙相距最远
③甲追上乙后，又被乙追上，乙先到达C地 ④甲追上乙后，先到达C地
其中正确的是 ．（请填上所有描述正确的序号）
（本小题满分12分）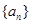
是等差数列，
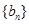是各项都为正数的等比数列，且
，
，
．
（Ⅰ）求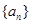、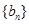的通项公式；
（Ⅱ）求数列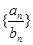
的前n项和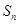
。
如图，三棱锥A—BPC中，AP⊥PC，AC⊥BC，M为AB中点，D为PB中点，且△PMB为正三角形．
（Ⅰ）求证：DM//平面APC；
（Ⅱ）求 证：平面ABC⊥平面APC；
（Ⅲ）若BC=4，AB=20，求三棱锥D—BCM的体积．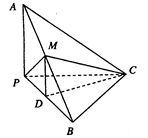
（本小题满分12分）已知函数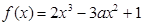
．
（1）若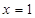
为函数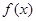
的一个极值点，试确定实数
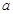的值，并求此时函数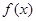的极值；
（2）求函数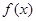的单调区间．
本小题满分12分）
对某校高一年级学生参加社区服务次数进行统计，随机抽取M名学生作为样本，得到这M名学生参加社区服务的次数．根据此数据作出了频数与频率的统计表和频率分布直方图如下：
| 分组 |
频数 |
频率 |
 |
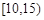10 |
0．25 |
 |
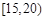25 |
 |
 |
 |
 |
 |
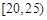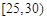2 |
0．05 |
| 合计 |
M |
1 |
（Ⅰ）求出表中
及图中
的值；
（Ⅱ）若该校高一学生有360人，试估计该校高一学生参加社区服务的次数在区间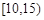内的人数；
（Ⅲ）在所取样本中，从参加社区服务的次数不少于20次的学生中任选2人，求至多一人参加社区服务次数在区间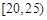内的概率．
在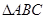
中，内角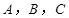
的对边分别是
，若
，
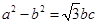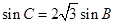，则
．