如图所示,在竖直平面内一足够长的光滑平行金属导轨MN、PQ相距L1=0.4m,放置在磁感应强度为B1=5T的匀强磁场中,磁场方向垂直于轨道平面向里,一质量为m=0.8kg的金属棒ab,垂直于MN、PQ紧贴在导轨上并与导轨接触良好,其接入在导轨间的电阻r=1Ω。金属导轨上端连接右侧的电路。R1=1.0Ω,R2=1.5Ω。R2两端通过细导线连接质量M=0.12kg的正方形金属框cdef,正方形边长L2=0.2m,每条边的电阻r0=1.0Ω,金属框处在一方向垂直纸面向里的磁感应强度B2=3T的匀强磁场中。现将金属棒由静止释放,不计其他电阻及摩擦,g取10m/s2。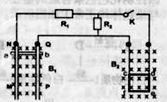
(1)将K断开,求棒下滑过程中达到的最大速率vm以及速率达到0.5vm时棒的加速度大小;
(2)将开关K闭合后,从棒释放到细导线刚好没有拉力的过程中,棒上产生的电热为2J,求此过程棒下滑的h。(结果保留两位有效数字)
半径为R的四分之一圆弧支架竖直放置,圆弧边缘C处有一小定滑轮,一根长度大于2R的轻绳两端系着质量分别为m1、m2的物体,挂在定滑轮两边,且m1>m2,开始时m1、m2均静止,可视为质点,不计一切摩擦。试求:
(1)若m1释放后一直沿圆弧轨道运动,求m1经过圆弧最低点A时的速度;
(2)为使m1能到达A点,m1与m2之间必须满足什么关系?
一个静止的 (原子质量为232.0372u),放出一个α粒子(原子质量为4.00260u)后,衰变为
(原子质量为232.0372u),放出一个α粒子(原子质量为4.00260u)后,衰变为 (原子质量为228.0287u)。假设放出的核能完全变为Th核和α粒子的动能,试计算α粒子的动能(1uc2=931.5MeV)。
(原子质量为228.0287u)。假设放出的核能完全变为Th核和α粒子的动能,试计算α粒子的动能(1uc2=931.5MeV)。
如图所示为一种获得高能粒子的装置。环形区域内存在垂直纸面向外,大小可调的匀强磁场。M、N为两块中心开有小孔的极板,每当带电粒子经过M、N板时,都会被加速,加速电压均为U;每当粒子飞离电场后,M、N板间的电势差立即变为零。粒子在M、N间的电场中一次次被加速,动能不断增大,而绕行半径R不变(M、N两极板间的距离远小于R)。当t=0时,质量为m,电荷量为+q的粒子静止在M板小孔处,
(1)求粒子绕行n圈回到M板时的动能En;
(2)为使粒子始终保持在圆轨道上运动,磁场必须递增;求粒子绕行第n圈时磁感应强度B的大小;
(3)求粒子绕行n圈所需总时间tn。
(15分)如图所示,一位质量为 m ="65" kg的特技演员,在进行试镜排练时,从离地面高 h1="6" m高的楼房窗口跳出后竖直下落,若有一辆平板汽车正沿着下落点正下方所在的水平直线上,以v0=" 6" m/s的速度匀速前进.已知该演员刚跳出时,平板汽车恰好运动到其前端距离下落点正下方3 m处,该汽车车头长2 m ,汽车平板长4.5 m,平板车板面离地面高 h2 ="1" m,人可看作质点,g取10 m/s2,人下落过程中未与汽车车头接触,人与车平板间的动摩擦因数μ=0.2.问:
(1)人将落在平板车上距车尾端多远处?
(2)假定人落到平板上后立即俯卧在车上不弹起,司机同时使车开始以大小为a=4 m/s2的加速度做匀减速直线运动,直至停止,则人是否会从平板车上滑下?
(3)人在货车上相对滑动的过程中产生的总热量Q为多少?
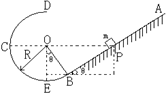
如图,AB是倾角为θ的粗糙直轨道,BCD是光滑的圆弧轨道,AB恰好在B点与圆弧相切,圆弧的半径为R。一个质量为m的物体(可以看作质点)从直轨道上的P点由静止释放,结果它能在两轨道间做往返运动。已知P点与圆弧的圆心o等高,物体与轨道AB间的动摩擦因数为μ。求
(1)物体第一次通过B点时的动能和经过圆弧轨道第一次回到B点时的动能;
(2)物体做往返运动的整个过程中在AB轨道上通过的总路程;
(3)最终当物体通过圆弧轨道最低点E时,对圆弧轨道的压力。