在平面直角坐标系xOy中，如图，已知椭圆C：
＋
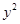＝1的上、下顶点分别为A、B，点P在椭圆C上且异于点A、B，直线AP、PB与直线l：y＝－2分别交于点M、N.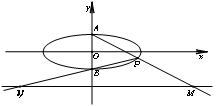
（1）设直线AP、PB的斜率分别为k1，k2，求证：k1·k2为定值；
（2）求线段MN长的最小值；
（3）当点P运动时，以MN为直径的圆是否经过某定点？请证明你的结论．
已知幂函数y＝x3m－9(m∈N*)的图象关于y轴对称，且在(0，＋∞)上是减函数．
(1)求m的值；
(2)求满足不等式(a＋1)－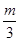
<(3－2a)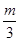－的实数a的取值范围．
若函数f(x)＝ax(a>1)的定义域和值域均为[m，n]，求实数a的取值范围．
设a＞0，f(x)＝
是R上的偶函数．
(1)求a的值；
(2)判断并证明函数f(x)在[0，＋∞)上的单调性；
(3)求函数的值域．
已知函数f(x)＝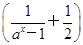
x3(a>0且a≠1)．
(1)求函数f(x)的定义域；
(2)讨论函数f(x)的奇偶性；
(3)求a的取值范围，使f(x)>0在定义域上恒成立．
画出函数y＝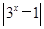
的图象，并利用图象回答：k为何值时，方程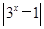＝k无解？有一个解？有两个解？