如图,已知空间四边形OABC,其对角线为OB、AC,M、N分别是对边OA、BC的中点,点G在线段MN上,且 =2
=2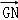 ,现用基向量
,现用基向量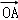 ,
,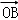 ,
,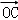 表示向量,设
表示向量,设 =x
=x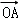 +y
+y +z
+z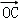 ,则x、y、z的值分别是()
,则x、y、z的值分别是()
A.x= ,y=
,y= ,z=
,z=
B.x= ,y=
,y= ,z=
,z=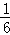
C.x= ,y=
,y= ,z=
,z=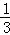
D.x= ,y=
,y=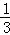 ,z=
,z=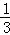
若向量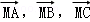 的起点与终点M、A、B、C互不重合且无三点共线,且满足下列关系(O为空间任一点),则能使向量
的起点与终点M、A、B、C互不重合且无三点共线,且满足下列关系(O为空间任一点),则能使向量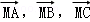 成为空间一组基底的关系是()
成为空间一组基底的关系是()
A. B.
B.
C.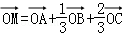 D.
D.
已知空间四边形ABCD的对角线为AC、BD,设G是CD的中点,则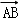 +
+ (
(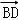 +
+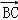 )等于()
)等于()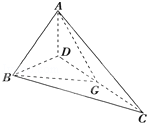
A.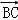 B.
B.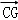 C.
C.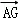 D.
D.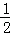
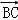
在平行六面体ABCD﹣A1B1C1D1中,设 ,则x+y+z等于()
,则x+y+z等于()
| A.1 | B. |
C.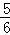 |
D. |
(理)在正方体ABCD﹣A1B1C1D1中,点E在A1C1上, 且
且 ,则()
,则()
A. |
B. |
C. |
D. |