现有10道题,其中6道甲类题,4道乙类题,张同学从中任取3道题解答.
(1)求张同学至少取到1道乙类题的概率;
(2)已知所取的3道题中有2道甲类题,1道乙类题.设张同学答对每道甲类题的概率都是 ,答对每道乙类题的概率都是
,答对每道乙类题的概率都是 ,且各题答对与否相互独立.用
,且各题答对与否相互独立.用 表示张同学答对题的个数,求
表示张同学答对题的个数,求 的分布列和数学期望.
的分布列和数学期望.
(本小题满分12分)
三棱锥 中,
中, ,
, ,
,
(1) 求证:面 面
面
(2) 求二面角 的余弦值.
的余弦值.
(本小题满分12分)
已知 ,其中向量
,其中向量 , (
, (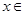 R).
R).
(1) 求 的最小正周期和最小值;
的最小正周期和最小值;
(2) 在△ABC中,角A、B、C的对边分别为 、
、 、
、 ,若
,若 ,a=2
,a=2 ,
, ,求边长
,求边长 的值.
的值.
(本小题15分)已知动圆 被y轴所截的弦长为2,被x轴分成两段弧,且弧长之比等于
被y轴所截的弦长为2,被x轴分成两段弧,且弧长之比等于 (其中
(其中 为圆心,O为坐标原点)。
为圆心,O为坐标原点)。
(1)求a,b所满足的关系式;
(2)点P在直线 上的投影为A,求事件“在圆P内随机地投入一点,使这一点恰好在
上的投影为A,求事件“在圆P内随机地投入一点,使这一点恰好在 内”的概率的最大值
内”的概率的最大值
(本小题13分)如图1,在三棱锥P—ABC中, 平面ABC,
平面ABC, ,D为侧棱PC上一点,它的正(主)视图和侧(左)视图如图2所示。
,D为侧棱PC上一点,它的正(主)视图和侧(左)视图如图2所示。
(1)证明: 平面PBC;
平面PBC;
(2)求三棱锥D—ABC的体积;
(3)在 的平分线上确定一点Q,使得
的平分线上确定一点Q,使得 平面ABD,并求此时PQ的长。
平面ABD,并求此时PQ的长。
(本小题13分)已知关于x的一元二次函数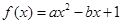 ,分别从集合P和Q中随机取一个数a和b得到数列
,分别从集合P和Q中随机取一个数a和b得到数列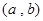 。
。
(1)若 ,
,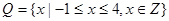 ,列举出所有的数对
,列举出所有的数对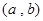 ,并求函数
,并求函数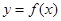 有零点的概率;
有零点的概率;
(2)若 ,
,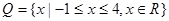 ,求函数
,求函数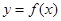 在区间
在区间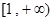 上是增函数的概率。
上是增函数的概率。