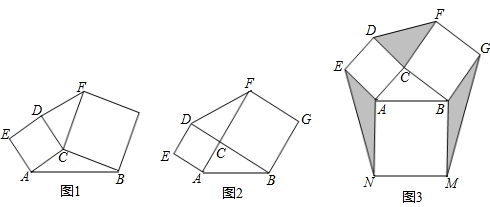
如图1，若分别以△ABC的AC、BC两边为边向外侧作的四边形ACDE和BCFG为正方形，则称这两个正方形为外展双叶正方形．
（1）发现：如图2，当∠C=90°时，求证：△ABC与△DCF的面积相等．
（2）引申：如果∠C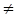
90°时，（1）中结论还成立吗？若成立，请结合图1给出证明；若不成立，请说明理由；
（3）运用：如图3，分别以△ABC的三边为边向外侧作的四边形ACDE、BCFG和ABMN为正方形，则称这三个正方形为外展三叶正方形．已知△ABC中，AC=3，BC=4．当∠C=_____度时，图中阴影部分的面积和有最大值是________．
，其中
.
互为相反数，
互为倒数，
的绝对值为
，求
的值.
的位置；