在数列{
}中，
="13" ，且前
项的算术平均数等于第项的2-1倍（∈N*）．
（1）写出此数列的前5项；
（2）归纳猜想{}的通项公式，并用数学归纳法证明．
（本小题满分12分）
设数列{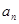
}的前n项和为
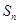，已知a1＝1，
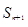＝2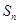＋n＋1（n∈N＋）
（Ⅰ）证明{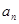＋1}是等比数列；
（Ⅱ）若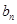
＝
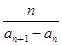，求数列{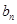}的前n项和
．
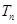（本小题满分12分）
如图所示，在四棱锥P－ABCD中，AB⊥AD，AD⊥DC，PA⊥底面ABCD，PA＝AD＝DC＝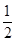
AB
＝1，M为PC的中点，N在AB上且AN＝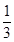
NB．
（Ⅰ）证明：MN∥平面PAD；
（Ⅱ）求三棱锥B－PNC的体积．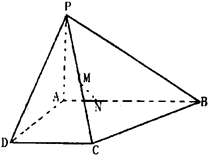
（本小题满分10分）
在△ABC中，a、b、c分别是角A、B、C的对边，向量
＝（2sinB，2－cos2B）,
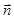＝（2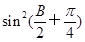
,－1），且⊥．
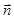（Ⅰ）求角B的大小；
（Ⅱ）若a＝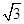
，b＝1，求c的值．
（文科）已知关于x的一元二次方程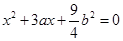
。
（Ⅰ）若
是从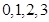
四个数中任取的一个数，
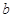是从
两个数中任取的一个数，求上述方程有实根的概率；
（Ⅱ）若是从区间
任取的一个数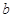，是从区间
任取的一个数，求上述方程有实根的概率。
（本题满分
分）（理科）在线段AD上任取不同于A，D的两点B，C，在B，C处折断此线段得到一条折线。求此折线能构成三角形的概率。