(本题满分12分)
已知直线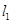 :
: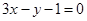 ,
,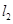 :
: ,求:
,求:
(1)直线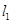 与
与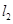 的交点
的交点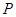 的坐标;(2)过点
的坐标;(2)过点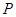 且与
且与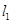 垂直的直线方程.
垂直的直线方程.
(本小题满分12分)
在正方体ABCD-A1B1C1D1中,E、F为棱AD、AB的中点.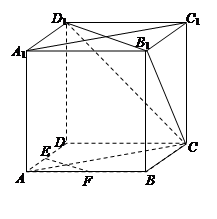
(1)求证:EF∥平面CB1D1;
(2)求证:平面CAA1C1⊥平面CB1D1
(本小题满分12分)如图,在四边形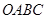 中,点C(1,3).
中,点C(1,3).
(1)求OC所在直线的斜率;
(2)过点C做CD⊥AB于点D,求CD所在直线的方程.
(满分14分) 定义在 上的函数
上的函数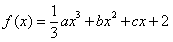 同时满足以下条件:
同时满足以下条件:
①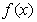 在
在 上是减函数,在
上是减函数,在 上是增函数;②
上是增函数;② 是偶函数;
是偶函数;
③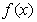 在
在 处的切线与直线
处的切线与直线 垂直.
垂直.
(1)求函数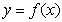 的解析式;
的解析式;
(2)设 ,求函数
,求函数 在
在 上的最小值.
上的最小值.
已知椭圆 (a>b>0)的离心率e=
(a>b>0)的离心率e=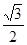 ,连接椭圆的四个顶点得到的菱形的面积为4.(Ⅰ)求椭圆的方程;(Ⅱ)设直线l与椭圆相交于不同的两点A、B,已知点A的坐标为(-
,连接椭圆的四个顶点得到的菱形的面积为4.(Ⅰ)求椭圆的方程;(Ⅱ)设直线l与椭圆相交于不同的两点A、B,已知点A的坐标为(- ,0).若
,0).若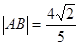 ,求直线l的倾斜角;
,求直线l的倾斜角;