如图,这是反映爷爷每天晚饭后从家中出发去元宝山公园锻炼的时间与距离之间关系的一幅图.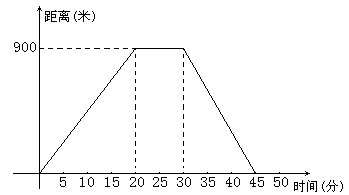
(1)右图反映的自变量、因变量分别是什么?
(2)爷爷每天从公园返回用多长时间?
(3)爷爷散步时最远离家多少米?
(4)爷爷在公园锻炼多长时间?
(5)计算爷爷离家后的2 0分钟内的平均速度.
请先阅读下列材料,然后解答问题:
解:因为: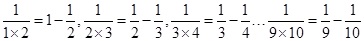
所以: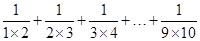
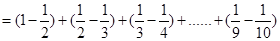
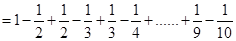
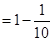
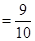
问题:
计算:(1)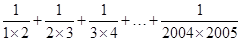 ;
;
(2)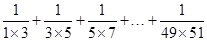
光明奶粉每袋标准质量为454克,在质量检测中,若超出标准质量2克记为+2克,若质量低于标准质量3克和3克以上,则这袋奶粉视为不合格产品,现抽取10袋样品进行质量检测,结果如下(单位:克):
| 袋号 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
| 记作 |
-2 |
0 |
1 |
-4 |
-3 |
-2 |
+2 |
+3 |
-5 |
-3 |
(1)这10袋奶粉中,有哪几袋不合格?
(2)质量最多的是哪袋?它的实际质量是多少?
(3)质量最少的是哪袋?它的实际质量是多少?
下面是一个正方体纸盒的展开图,请把-10,7,10,-2,-7,2分别填入六个正方形,使得按虚线折成正方体后,相对面上的两数互为相反数。

比较下列各组数的大小.
(1) 与
与
(2) ,
, ,
, , 0.
, 0.
七年级一班某次数学测验的平均成绩为80分,数学老师以平均成绩为基准,记作0,把小龙、小聪、小梅、小莉、小刚这五位同学的成绩简记为+10,–15,0,+20,–2.问这五位同学的实际成绩分别是多少分?