已知某高中高一800名学生某次考试的数学成绩，现在想知道不低于120分，90～
120分，75～90分，60～75分，60分以下的学生分别占多少，需要做的工作是( )
| A．抽取样本，据样本估计总体 | B．求平均成绩 |
| C．进行频率分布 | D．计算方差 |
设数列
的前n项和为
，令
，称
为数列
，
，，
的“理想数”，已知数列，，，
的“理想数”为2004，那么数列12， ，，，的“理想数”为（ ）
| A．2002 | B．2004 | C．2008 | D．2012 |
设
，则有（）
A． |
B． |
C． |
D． |
下图给出的是计算
的值的一个程序框图，其中判断框内应填入的条件是( )
| A．i<10 | B．i>10 | C．i>20 | D．i<20 |
设直线l经过点M（1,5）、倾斜角为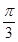
，则直线l的参数方程可为( )
A． |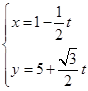
B． |
C． |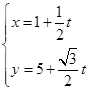
D． |
某种产品的广告费支出
与销售额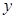
（单位：万元）之间有下表关系
|
2 |
4 |
5 |
6 |
8 |
|
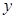30 |
40 |
60 |
50 |
70 |
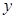与的线性回归方程为
，当广告支出5万元时，随机误差的效应（残差）为 （ ）
A．10 B．20 C．30 D．40