如图，抛物线y=ax2 + bx + c 交x轴于A、B两点，交y轴于点C，对称轴为直线x=1,已知：A(-1,0)、C(0,-3)。
（1）求抛物线y= ax2 + bx + c 的解析式；
（2）求△AOC和△BOC的面积比；
（3）在对称轴上是否存在一个P点,使△PAC的周长最小。若存在，请你求出点P的坐标；若不存在，请你说明理由。
化简：
⑴
(5分)
（2）
(5分)
解不等式组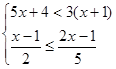
， 并且把解集在数轴上表示出来。
解不等式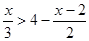
。
某学校组织八年级学生参加社会实践活动，若单独租用35座客车若干辆，则刚好坐满；若单独租用55座客车，则可以少租一辆，且余45个空座位．
（1）求该校八年级学生参加社会实践活动的人数；
（2）已知35座客车的租金为每辆320元，55座客车的租金为每辆400元．根据租车资金不超过1500元的预算，学校决定同时租用这两种客车共4辆（可以坐不满）．请你计算本次社会实践活动所需车辆的租金．
装卸工人往一辆大型运货车上装载货物．装完货物所需时间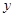
（min）与装载速度
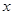（t/min）之间的函数关系如图：
⑴这批货物的质量是多少？
⑵写出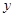与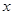之间的函数关系式；
⑶货车到达目的地后开始卸货，如果以1.5t/min的速度卸货，需要多长时间才能卸完货物？