已知函数
，
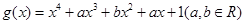，（1）若
的最小值为2，求
值；（2）设函数
有零点，求
的最小值.
在△ABC中，内角A、B、C的对边分别是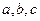
，
，
，
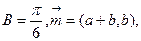
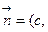
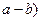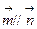(1)求内角A;
(2)求函数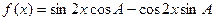
的最小正周期，并写出它的单调增区间。
（本小题满分14分）
设函数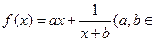
Z），曲线
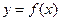在点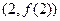
处的切线方程为
。
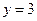（1）求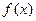
的解析式；
（2）证明：函数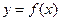的图象是一个中心对称图形，并求其对称中心；
（3）证明：曲线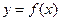上任一点的切线与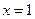直线
和直线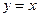
所围三角形的面积为定值，并求出此定值。
（本小题满分14分）
如图所示，已知曲线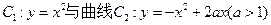
交于点O、A，直线
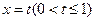与曲线
、
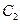分别交于点D、B，连结OD，DA，AB.
（1）求证:曲边四边形ABOD（阴影部分：OB为抛物线弧）的面积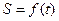
的函数表达式为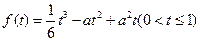
（2）求函数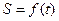在区间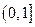
上的最大值.
（本小题满分13分）
甲、乙两人各射击一次，击中目标的概率分别是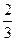
和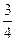
，假设两个射击是否击中目标，相互之间没有影响；每人各次射击是否中目标相互之间也没有影响。
（1）求甲射击4次，至少有1次未击中目标的概率；
（2）求两人各射击4次，甲恰好击中目标2次且乙恰好击中目标3次的概率；
（3）假设某人连续2次未击中目标，则中止其射击。则乙恰好射击5次后被中止射击的概率是多少？
（本小题满分13分）
设函数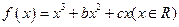
，已知
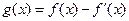是奇函数.
（Ⅰ）求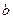
、
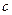的值;（Ⅱ）求
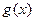的单调区间与极值.