在平面直角坐标系xOy中,点P是圆 上一动点,
上一动点, x轴于点D.记满足
x轴于点D.记满足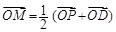 的动点M的轨迹为Γ.
的动点M的轨迹为Γ.
(1)求轨迹Γ的方程;
(2)已知直线 与轨迹Γ交于不同两点A,B,点G是线段AB中点,射线OG交轨迹Γ于点Q,且
与轨迹Γ交于不同两点A,B,点G是线段AB中点,射线OG交轨迹Γ于点Q,且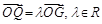 .
.
①证明:
②求△AOB的面积S(λ)的解析式,并计算S(λ)的最大值.
(本小题满分12分)如图所示,已知A(1,3),B(-1,-1),C(2,1).求△ABC的BC边上的高所在的直线方程.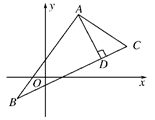
(本小题满分12分)已知圆
 与
与 轴相切.
轴相切.
(1)求 的值;
的值;
(2)若圆 的切线在
的切线在 轴和
轴和 轴上的截距相等,求该切线方程;
轴上的截距相等,求该切线方程;
(3)从圆外一点 向圆引切线,M为切点,O为坐标原点,且有
向圆引切线,M为切点,O为坐标原点,且有 ,求使
,求使 最小的点P的坐标.
最小的点P的坐标.
(本小题满分12分)已知关于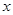 的不等式
的不等式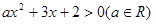
(1)若不等式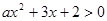 的解集为
的解集为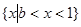 ,求
,求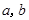 的值.
的值.
(2)求关于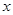 的不等式
的不等式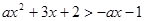
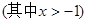 的解集
的解集
(本小题满分12分)如图所示,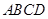 是正方形,
是正方形,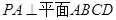 ,
,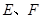 是
是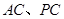 的中点.
的中点.
(1)求证: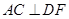 ;
;
(2)若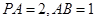 ,求三棱锥
,求三棱锥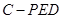 的体积.
的体积.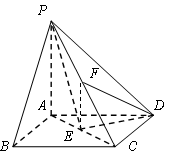
(本小题满分12分)已知向量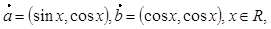 函数
函数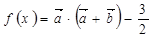 。
。
(1)求函数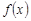 的最小正周期和最大值.
的最小正周期和最大值.
(2)求函数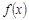 的单调递增区间.
的单调递增区间.