天水市某校为了开展“阳光体育”活动,需购买某一品牌的羽毛球,甲、乙两超市均以每只3元的价格出售,并对一次性购买这一品牌羽毛球不低于100只的用户均实行优惠:甲超市每只羽毛球按原价的八折出售;乙超市送15只羽毛球后其余羽毛球每只按原价的九折出售.
(1)请你任选一超市,一次性购买x(x≥100且x为整数)只该品牌羽毛球,写出所付钱y(元)与x之间的函数关系式.
(2)若共购买260只该品牌羽毛球,其中在甲超市以甲超市的优惠方式购买一部分,剩下的又在乙超市以乙超市的优惠方式购买.购买260只该品牌羽毛球至少需要付多少元钱?这时在甲、乙两超市分别购买该品牌羽毛球多少只?
如图,一轮船由B处向C处航行,在B处测得C处在B的北偏东75°方向上,在海岛上的观察所A测得B在A的南偏西30°方向上,C在A的南偏东25°方向。若轮船行驶到C处,那么从C处看A,B两处的视角∠ACB是多少度?
(本题6分)如图,AD为△ABC的中线,BE为△ABD的中线。
(1)∠ABE=15°,∠BAD=40°,求∠BED的度数;
(2)在△BED中作BD边上的高;
(3)若△ABC的面积为40,BD=5,则点E到BC边的距离为多少?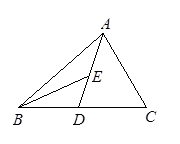
如图,直线DE交△ABC的边AB、AC于D、E,交BC延长线于F,若∠B=67°,∠ACB=74°,∠AED=48°,求∠BDF的度数.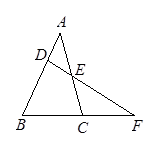
解下列方程组:
⑴、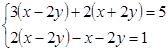 ⑵、
⑵、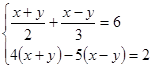
( 7分)如图,AB∥CD,分别写出下面四个图形中∠A与∠P、∠C的关系,请你从所得到的关系中任选一图的结论说明理由。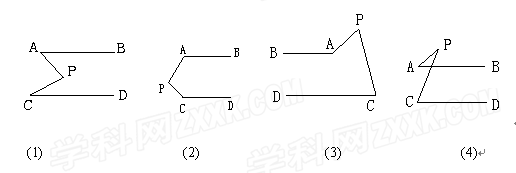
⑴⑵
⑶⑷