如图,AB∥FC,D是AB上一点,DF交AC于点E,DE=FE,分别延长FD和CB交于点G.
(1) 求证:△ADE≌△CFE;
(2) 若GB=2,BC=4,BD=1,求AB的长.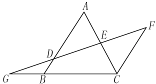
某池塘里养了鱼苗1万条,根据这几年的经验,鱼苗成活率为95%,一段时间后准备打捞出售,第一网捞出40条,称得平均每条鱼重2.5千克,第二网捞出25条,称得平均每条鱼重2.2千克,第三网捞出35条,称得平均每条鱼重2.8千克,试估计这池塘中鱼的质量.
如图,已知正方形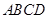 中,点
中,点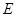 是
是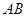 上的一点,连结
上的一点,连结 ,以
,以 为一边,在
为一边,在 的上方作正方形
的上方作正方形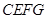 ,连结
,连结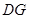 .求证:
.求证: .
.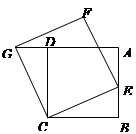
如图,小赵和路人在路灯下行走,试确定图中路灯灯泡的位置,并画出小赵在灯光下的影子.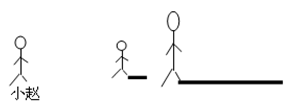
解方程: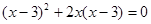 .
.
如图,在平面直角坐标系xOy中,将抛物线C1:y=x2+3先向右平移1个单位,再向下平移7个单位得到抛物线C2。C2的图象与x轴交于A、B两点(点A在点B的左侧)。
(1)求抛物线C2的解析式;
(2)若抛物线C2的对称轴与x轴交于点C,与抛物线C2交于点D,与抛物线C1交于点E,连结AD、DB、BE、EA,请证明四边形ADBE是菱形,并计算它的面积;
(3)若点F为对称轴DE上任意一点,在抛物线C2上是否存在这样的点G,使以O、B、F、G四点为顶点的四边形是平行四边形,如果存在,请求出点G的坐标,如果不存在,请说明理由。