在求1+62+63+64+65+66+67+68+69的值时，小林发现：从第二个加数起每一个加数都是前一个加数的6倍，于是她设：
S=1+62+63+64+65+66+67+68+69①
然后在①式的两边都乘以6，得：
6S=6+62+63+64+65+66+67+68+69+610②
②﹣①得6S﹣S=610﹣1，即5S=610﹣1，所以S=
，得出答案后，爱动脑筋的小林想：
如果把“6”换成字母“a”（a≠0且a≠1），能否求出1+a+a2+a3+a4+…+a2014的值？你的答案是（ ）
A． |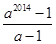
B． |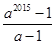
C． |
D．a2014﹣1 |
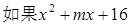是一个完全平方式，那么m等于（）
| A．4 | B． |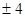
C．8 | D． |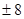
在边长为a的正方形中挖去一个边长为b的小正方形（a>b）（左图），把余下的部分拼成一个矩形（右图），根据两个图形中阴影部分的面积相等，可以验证（）
A． |
B． |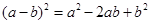
C． |
D． |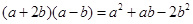
在实数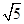
、
、0、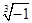
、
、
、
、
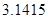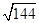、2.123122312233…… 中，无理数的个数为（）
| A．2个 | B．3个 | C．4个 | D．5个 |
若2m-4与3m-1是同一个正数的平方根，则m为（）
| A．－３ | B．１ | C．－１ | D．－３或１ |
在下列说法中 ①有理数和数轴上点一一对应；②不带根号的数一定是有理数；③负数没有立方根；④
是17的平方根，其中正确的有（）
| A．1个 | B．2个 | C．3个 | D．4个 |