如图,在平行四边形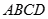 中,
中,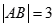 ,
, ,
,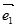 =
=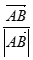 ,
,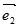 =
=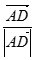 ,
,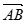 与
与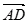 的夹角为
的夹角为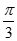 .
.
(1)若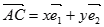 ,求
,求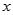 、
、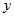 的值;
的值;
(2)求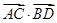 的值;
的值;
(3)求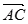 与
与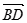 的夹角的余弦值.
的夹角的余弦值.
已知函数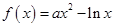 (
(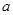 为常数).
为常数).
(1)当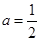 时,求
时,求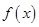 的单调递减区间;
的单调递减区间;
(2)若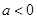 ,且对任意的
,且对任意的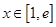 ,
,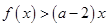 恒成立,求实数
恒成立,求实数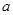 的取值范围.
的取值范围.
已知椭圆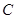 的中心在坐标原点,右准线为
的中心在坐标原点,右准线为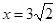 ,离心率为
,离心率为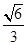 .若直线
.若直线 与椭圆
与椭圆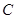 交于不同的两点
交于不同的两点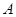 、
、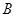 ,以线段
,以线段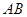 为直径作圆
为直径作圆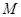 .
.
(1)求椭圆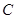 的标准方程;
的标准方程;
(2)若圆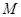 与
与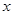 轴相切,求圆
轴相切,求圆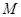 被直线
被直线 截得的线段长.
截得的线段长.
如图,四棱锥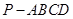 的底面为平行四边形,
的底面为平行四边形,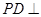 平面
平面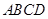 ,
, 为
为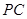 中点.
中点.
(1)求证: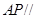 平面
平面 ;
;
(2)若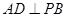 ,求证:
,求证: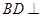 平面
平面 .
.
在锐角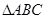 中,
中,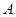 、
、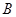 、
、 所对的边分别为
所对的边分别为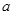 、
、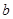 、
、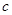 .已知向量
.已知向量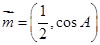 ,
, ,且
,且 .
.
(1)求角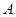 的大小;
的大小;
(2)若 ,
,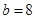 ,求
,求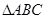 的面积.
的面积.
将编号为1,2,3,4的四个小球,分别放入编号为1,2,3,4的四个盒子,每个盒子中有且仅有一个小球.若小球的编号与盒子的编号相同,得1分,否则得0分.记 为四个小球得分总和.
为四个小球得分总和.
(1)求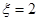 时的概率;
时的概率;
(2)求 的概率分布及数学期望.
的概率分布及数学期望.